题目内容
已知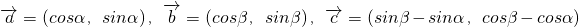
，0＜α＜β＜π，若＜
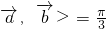且
，求α的值．
解：cos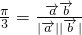
=cos（β-α）
∵0＜β-α＜π
∴β-α=
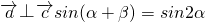
∵β=α+
∴sin（α+β）=sin（2α+）=sin2α
?sin（2α-）=0
0＜α＜β＜π?0＜2β＜2π
?2α-
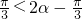=2β-π
?-
＜π
?2α-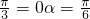
．
分析：通过
与
的数量积，推出α，β的关系，然后利用，得到α，β的关系，然后求解α的值即可．
点评：本题通过向量的数量积，向量的垂直求出推出角的大小，考查方程思想和计算能力．
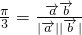=cos（β-α）∵0＜β-α＜π
∴β-α=
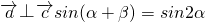
∵β=α+
∴sin（α+β）=sin（2α+
）=sin2α?sin（2α-
）=00＜α＜β＜π?0＜2β＜2π
?2α-
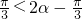=2β-π?-
＜π?2α-
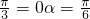．分析：通过
与的数量积，推出α，β的关系，然后利用，得到α，β的关系，然后求解α的值即可．点评：本题通过向量的数量积，向量的垂直求出推出角的大小，考查方程思想和计算能力．
练习册系列答案
相关题目
已知α∈（0，π），且sinα+cosα=
，则cosα的值为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|