题目内容
10．函数f（x）=sin（2x+5m）（m＞0）的图象关于y轴对称，则m的最小值为$\frac{π}{10}$．分析 由条件利用正弦函数、余弦函数的图象的对称性可得5m=kπ+$\frac{π}{2}$，k∈z，由此求得m的最小值．
解答 解：函数f（x）=sin（2x+5m）的图象关于y轴对称，则5m=kπ+$\frac{π}{2}$，k∈z，
即m=$\frac{kπ}{5}$+$\frac{π}{10}$，则m的最小值为$\frac{π}{10}$，
故答案为：$\frac{π}{10}$．
点评 本题主要考查正弦函数、余弦函数的图象的对称性，属于基础题．
练习册系列答案
相关题目
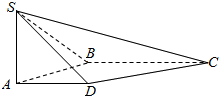如图，在四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠ABC=90°，SA=AB=AD=1，BC=2．
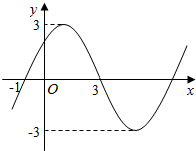函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈[0，2π]）的图象如图所示，试求该函数的振幅、频率和初相．
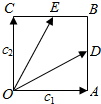如图所示，四边形OABC是边长为1的正方形，$\overrightarrow{OA}$=e1，$\overrightarrow{OC}$=e2，D、E分别为AB、BC中点．
15．若sin（π-α）=log8$\frac{1}{4}$，则cos（π+α）的值为（ ）
| A． | $\frac{\sqrt{5}}{3}$ | B． | -$\frac{\sqrt{5}}{3}$ | C． | ±$\frac{\sqrt{5}}{3}$ | D． | 以上都不对 |
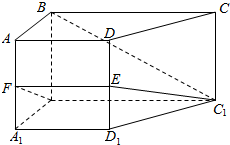如图所示，在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中，AD∥BC，AD⊥AB，AB═$\sqrt{2}$，AD=2，BC=4，AA1=2，E，F分别是DD1，AA1的中点．