题目内容
设实数a,b满足lg(a-1)+lg(b-1)=lg4,则a•b的取值范围是 .
【答案】分析:首先由对数的性质可得a>1、b>1,结合对数的运算性质可将lg(a-1)+lg(b-1)=lg4变形为ab-(a+b)-3=0,结合基本不等式可得ab-2 -3≥0,运用换元法,令t=
-3≥0,运用换元法,令t= ,可得t2-2t-3≥0,解此方程并结合可得t的范围可得t≥3,转化可得ab≥9,即可得答案.
,可得t2-2t-3≥0,解此方程并结合可得t的范围可得t≥3,转化可得ab≥9,即可得答案.
解答:解:根据题意,lg(a-1)+lg(b-1)=lg4,有a-1>0,b-1>0,即a>1、b>1,
lg(a-1)+lg(b-1)=lg4⇒lg(a-1)(b-1)=lg4⇒(a-1)(b-1)=4,
即ab-(a+b)+1=4,变形可得ab-(a+b)-3=0,①
又由a+b≥2 ,
,
将其代入①可得,ab-2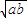 -3≥0,
-3≥0,
令t= ,则t>1,可得t2-2t-3≥0,
,则t>1,可得t2-2t-3≥0,
解可得t≥3或t≤-1,
又由t>1,则t≥3,即 ≥3,则ab≥9,
≥3,则ab≥9,
则a•b的取值范围是[9,+∞);
故答案为[9,+∞).
点评:本题考查基本不等式的应用,涉及对数运算性质,注意结合对数的性质,分析出a>1、b>1.
 -3≥0,运用换元法,令t=
-3≥0,运用换元法,令t= ,可得t2-2t-3≥0,解此方程并结合可得t的范围可得t≥3,转化可得ab≥9,即可得答案.
,可得t2-2t-3≥0,解此方程并结合可得t的范围可得t≥3,转化可得ab≥9,即可得答案.解答:解:根据题意,lg(a-1)+lg(b-1)=lg4,有a-1>0,b-1>0,即a>1、b>1,
lg(a-1)+lg(b-1)=lg4⇒lg(a-1)(b-1)=lg4⇒(a-1)(b-1)=4,
即ab-(a+b)+1=4,变形可得ab-(a+b)-3=0,①
又由a+b≥2
 ,
,将其代入①可得,ab-2
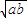 -3≥0,
-3≥0,令t=
 ,则t>1,可得t2-2t-3≥0,
,则t>1,可得t2-2t-3≥0,解可得t≥3或t≤-1,
又由t>1,则t≥3,即
 ≥3,则ab≥9,
≥3,则ab≥9,则a•b的取值范围是[9,+∞);
故答案为[9,+∞).
点评:本题考查基本不等式的应用,涉及对数运算性质,注意结合对数的性质,分析出a>1、b>1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目