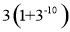题目内容
7.△ABC中,BC=3,∠C=90°,∠A的平分线交BC于D.若BD=2DC,则△ABC面积是$\frac{3\sqrt{3}}{2}$.分析 由已知解得CD=1,BD=2,由D点向AB引垂线,设垂足为E,可求DE=1,BE=$\sqrt{3}$,AC=AE,由$\frac{AC}{AB}=\frac{CD}{BD}=\frac{1}{2}=\frac{AC}{AC+\sqrt{3}}$,解得:AC=$\sqrt{3}$,根据三角形面积公式即可得解.
解答 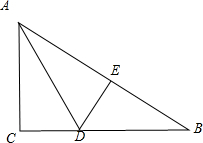 解:∵BC=3,BD=2DC,
解:∵BC=3,BD=2DC,
∴可得:CD=1,BD=2,
由D点向AB引垂线,设垂足为E,
∵∠A的平分线交BC于D.则DE=1,BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=$\sqrt{4-1}$=$\sqrt{3}$,
∵△ACD≌△AED,可得:AC=AE,
∴$\frac{AC}{AB}=\frac{CD}{BD}=\frac{1}{2}=\frac{AC}{AC+\sqrt{3}}$,解得:AC=$\sqrt{3}$,
∴S△ABC=S△ACD+S△ABD=$\frac{1}{2}AC•CD$+$\frac{1}{2}AB•DE$=$\frac{1}{2}×\sqrt{3}×1$+$\frac{1}{2}×2\sqrt{3}×1$=$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题主要考查了角平分线的性质,勾股定理,全等三角形的性质,三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
2.幂函数f(x)过点(4,2),则f(16)的值为( )
| A. | 4 | B. | 2 | C. | ±4 | D. | 3 |
12.在复平面内,O为原点,向量$\overrightarrow{OA}$对应的复数为-1-2i,若点A关于直线y=-x的对称点为B,则向量$\overrightarrow{OB}$对应的复数为( )
| A. | -2-i | B. | 1+2i | C. | 2+i | D. | -1+2i |
16.己知f(x)=x2-2x+2,在[$\frac{1}{4}$,m2-m+2]上任取三个数a,b,c,均存在以 f(a),f(b),f(c)为三边的三角形,则m的取值范围为( )
| A. | (0,1) | B. | [0,$\frac{\sqrt{2}}{2}$) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
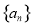 满足
满足 ( )
( ) B.
B.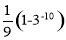 C.
C. D.
D.