题目内容
11.直线y=$\sqrt{3}$x+1的倾斜角为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 根据直线的倾斜角与斜率的关系,结合倾斜角的取值范围即可求出答案.
解答 解:设直线y=$\sqrt{3}$x+1的倾斜角为α,
则tanα=$\sqrt{3}$,其中α∈[0°,180°);
∴α=60°.
故选:B.
点评 本题考查了根据直线的方程求倾斜角的应用问题,是基础题目.

练习册系列答案
相关题目
2.复平面上表示复数z=1-i(i为虚数单位)的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.抛物线x2=2y的焦点到准线的距离是( )
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
16.如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,E为线段CD上一动点,现将△AED沿AE折起,使平面AED⊥平面ABC,当E从D运动到C,则D在平面ABC上的射影K所形成轨迹的长度为( )
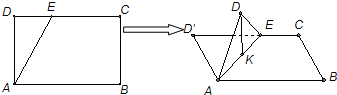

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
1.点A在点B的上方,从A看B的俯角为α,从B看A的仰角为β,则( )
| A. | α=β | B. | α+β=$\frac{π}{2}$ | C. | α+β=π | D. | α>β |
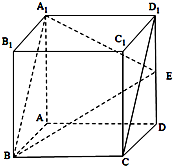 如图所示,正方体ABCD-A1B1C1D1的棱长为1,E是棱DD1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,E是棱DD1的中点.