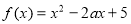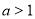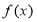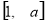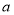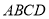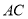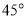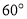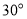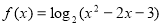题目内容
已知圆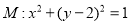 ,设点
,设点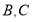 是直线
是直线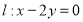 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是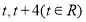 ,点
,点 在线段
在线段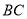 上,过
上,过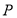 点作圆
点作圆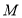 的切线
的切线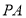 ,切点为
,切点为 .
.
(1)若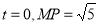 ,求直线
,求直线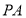 的方程;
的方程;
(2)经过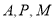 三点的圆的圆心是
三点的圆的圆心是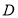 ,求线段
,求线段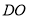 (
(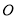 为坐标原点)长的最小值
为坐标原点)长的最小值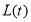 .
.
(1)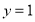 或
或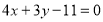 ;(2)
;(2) .
.
【解析】
试题分析:(1)因为点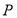 在线段
在线段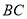 上,所以可假设点
上,所以可假设点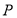 的坐标,又根据
的坐标,又根据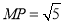 ,所以可求出点
,所以可求出点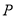 的坐标,同时要检验一下使得点
的坐标,同时要检验一下使得点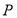 符合在线段
符合在线段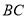 上,再通过假设直线的斜率,利用点到直线的距离等于圆的半径即可求出直线的斜率,从而得到切线方程;(2)因为经过
上,再通过假设直线的斜率,利用点到直线的距离等于圆的半径即可求出直线的斜率,从而得到切线方程;(2)因为经过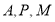 三点的圆的圆心是
三点的圆的圆心是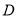 ,求线段
,求线段 (
( 为坐标原点)长,通过假设点
为坐标原点)长,通过假设点 的坐标即可表示线段
的坐标即可表示线段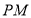 的中点
的中点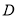 的坐标(因为
的坐标(因为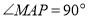 ), 根据两点间的距离公式写出
), 根据两点间的距离公式写出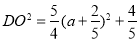 的表达式,接着关键是根据
的表达式,接着关键是根据 的范围讨论,因为
的范围讨论,因为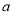 的值受
的值受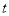 的大小决定的,要分三种情况讨论即i)
的大小决定的,要分三种情况讨论即i) 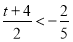 ;ii)
;ii) 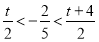 ;iii)
;iii) 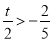 ;分别求出三种情况的最小值即为所求的结论.
;分别求出三种情况的最小值即为所求的结论.
试题解析:(1)设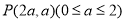

解得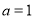 或
或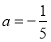 (舍去)
(舍去)
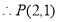
由题意知切线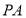 的斜率存在,设斜率为
的斜率存在,设斜率为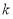
所以直线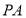 的方程为
的方程为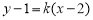 ,即
,即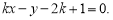
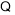 直线
直线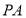 与圆
与圆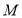 相切,
相切,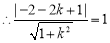 ,解得
,解得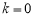 或
或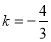
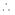 直线
直线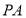 的方程是
的方程是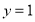 或
或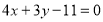 6分
6分
(2)设
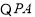 与圆
与圆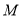 相切于点
相切于点

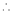 经过
经过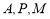 三点的圆的圆心
三点的圆的圆心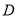 是线段
是线段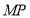 的中点
的中点
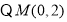
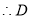 的坐标是
的坐标是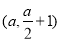
设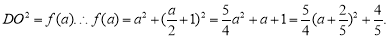
当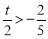 ,即
,即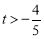 时,
时,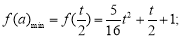
当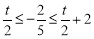 ,即
,即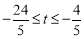 时,
时,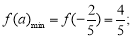
当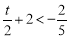 ,即
,即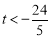 时,
时,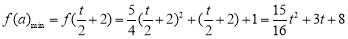
则 .
.
考点:1.直线与圆的位置关系;2.点到直线的距离公式;3.动区间的二次函数的最值问题;4.分类讨论的思想.

练习册系列答案
相关题目