题目内容
已知向量 ,若
,若 ,则实数
,则实数 = .
= .
8
【解析】
试题分析:因为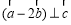 ,所以
,所以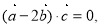 而
而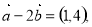 所以
所以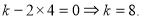 向量的数量积的坐标表示
向量的数量积的坐标表示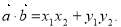
考点:向量的数量积,向量的垂直的坐标表示.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
题目内容
已知向量 ,若
,若 ,则实数
,则实数 = .
= .
8
【解析】
试题分析:因为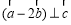 ,所以
,所以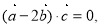 而
而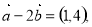 所以
所以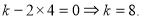 向量的数量积的坐标表示
向量的数量积的坐标表示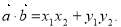
考点:向量的数量积,向量的垂直的坐标表示.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案