题目内容
设抛物线C:y2=2px(p>0)的焦点为F,过F且垂直于x轴的直线与抛物线交于P1,P2两点,已知|P1P2|=8.(1)求抛物线C的方程;
(2)设m>0,过点M(m,0)作方向向量为
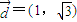 的直线与抛物线C相交于A,B两点,求使∠AFB为钝角时实数m的取值范围;
的直线与抛物线C相交于A,B两点,求使∠AFB为钝角时实数m的取值范围;(3)①对给定的定点M(3,0),过M作直线与抛物线C相交于A,B两点,问是否存在一条垂直于x轴的直线与以线段AB为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由.
②对M(m,0)(m>0),过M作直线与抛物线C相交于A,B两点,问是否存在一条垂直于x轴的直线与以线段AB为直径的圆始终相切?(只要求写出结论,不需用证明)
【答案】分析:(1)根据|P1P2|=8,可得2p=8,从而可得抛物线C的方程;
(2)直线方程代入y2=8x得一元二次方程,用坐标表示向量,利用∠AFB为钝角,可得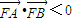 ,从而可得不等式,由此可求实数m的取值范围;
,从而可得不等式,由此可求实数m的取值范围;
(3)①设过M所作直线方程为y=k(x-3)代入y2=8x,求出|AB|,设存在直线x=x满足条件,则可得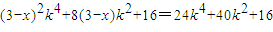 对任意k恒成立,此时直线不存在;②对参数m讨论,可得结论.
对任意k恒成立,此时直线不存在;②对参数m讨论,可得结论.
解答:解:(1)由条件得2p=8,∴抛物线C的方程为y2=8x;….(4分)
(2)直线方程为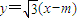 代入y2=8x得3x2-(6m+8)x+3m2=0,
代入y2=8x得3x2-(6m+8)x+3m2=0,
设A(x1,y1),B(x2,y2),F(2,0),则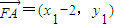 ,
,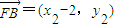 ,
,
∴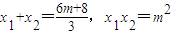 .….(6分)
.….(6分)
∵∠AFB为钝角,∴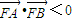 ,∴(x1-2)(x2-2)+y1y2<0,
,∴(x1-2)(x2-2)+y1y2<0,
即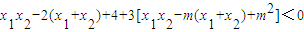 ,
,
∴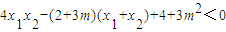 ,….(8分)
,….(8分)
因此3m2-36m-4<0,∴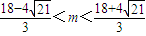 ,
,
又由m>0,则综上可得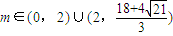 .….(10分)
.….(10分)
(3)①设过M所作直线方程为y=k(x-3)代入y2=8x得ky2-8y-24k=0,….(11分)
设A(x1,y1),B(x2,y2),则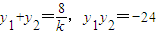 ,
,
∴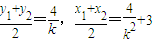 ,∴AB中点
,∴AB中点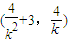 ,….(12分)
,….(12分)
∴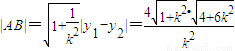 .….(13分)
.….(13分)
设存在直线x=x满足条件,则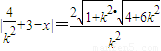 ,….(14分)
,….(14分)
∴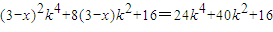 对任意k恒成立,
对任意k恒成立,
∴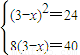 无解,∴这样的直线不存在. ….(16分)
无解,∴这样的直线不存在. ….(16分)
②当m=2时,存在直线x=-2满足条件;….(17分)
当m≠2且m>0时,直线不存在. ….(18分)
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查向量知识的运用,正确运用韦达定理是关键.
(2)直线方程代入y2=8x得一元二次方程,用坐标表示向量,利用∠AFB为钝角,可得
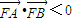 ,从而可得不等式,由此可求实数m的取值范围;
,从而可得不等式,由此可求实数m的取值范围;(3)①设过M所作直线方程为y=k(x-3)代入y2=8x,求出|AB|,设存在直线x=x满足条件,则可得
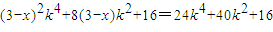 对任意k恒成立,此时直线不存在;②对参数m讨论,可得结论.
对任意k恒成立,此时直线不存在;②对参数m讨论,可得结论.解答:解:(1)由条件得2p=8,∴抛物线C的方程为y2=8x;….(4分)
(2)直线方程为
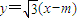 代入y2=8x得3x2-(6m+8)x+3m2=0,
代入y2=8x得3x2-(6m+8)x+3m2=0,设A(x1,y1),B(x2,y2),F(2,0),则
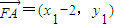 ,
,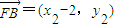 ,
,∴
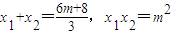 .….(6分)
.….(6分)∵∠AFB为钝角,∴
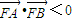 ,∴(x1-2)(x2-2)+y1y2<0,
,∴(x1-2)(x2-2)+y1y2<0,即
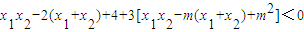 ,
,∴
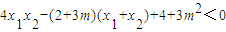 ,….(8分)
,….(8分)因此3m2-36m-4<0,∴
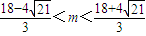 ,
,又由m>0,则综上可得
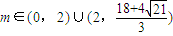 .….(10分)
.….(10分)(3)①设过M所作直线方程为y=k(x-3)代入y2=8x得ky2-8y-24k=0,….(11分)
设A(x1,y1),B(x2,y2),则
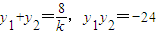 ,
,∴
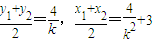 ,∴AB中点
,∴AB中点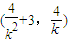 ,….(12分)
,….(12分)∴
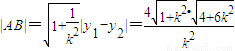 .….(13分)
.….(13分)设存在直线x=x满足条件,则
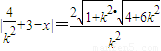 ,….(14分)
,….(14分)∴
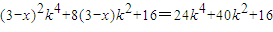 对任意k恒成立,
对任意k恒成立,∴
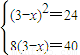 无解,∴这样的直线不存在. ….(16分)
无解,∴这样的直线不存在. ….(16分)②当m=2时,存在直线x=-2满足条件;….(17分)
当m≠2且m>0时,直线不存在. ….(18分)
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查向量知识的运用,正确运用韦达定理是关键.

练习册系列答案
相关题目