题目内容
2．球的体积与其表面积的数值相等，则球的表面积等于（ ）| A． | π | B． | 4π | C． | 16π | D． | 36π |
分析 设出球的半径，求出球的体积和表面积，利用相等关系求出球的半径，即可求出球的表面积．
解答 解：设球的半径为r，则球的体积为：$\frac{4}{3}π{r}^{3}$，球的表面积为：4πr2
因为球的体积与其表面积的数值相等，所以$\frac{4}{3}π{r}^{3}$=4πr2．
解得r=3
所以4πr2=36π．
故选：D．
点评 本题考查球的体积与表面积的计算，是基础题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
10．复数$\frac{1+2i}{3-4i}$的虚部为（ ）
| A． | $-\frac{1}{5}$ | B． | $-\frac{i}{5}$ | C． | $\frac{2i}{5}$ | D． | $\frac{2}{5}$ |
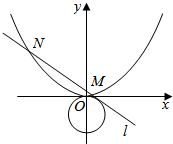已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1）．