题目内容
已知抛物线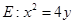 .
.
(1)若直线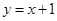 与抛物线
与抛物线 相交于
相交于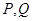 两点,求
两点,求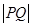 弦长;
弦长;
(2)已知△ 的三个顶点在抛物线
的三个顶点在抛物线 上运动.若点
上运动.若点 在坐标原点,
在坐标原点, 边过定点
边过定点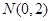 ,点
,点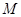 在
在 上且
上且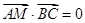 ,求点
,求点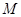 的轨迹方程.
的轨迹方程.
(1)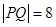 ;(2)
;(2)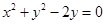 (
(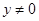 ).
).
解析试题分析:(1)这是解析几何中的常规问题,注意设而不求思想方法的使用;(2)求轨迹方程的方法有:直接法、定义法、代入转移法、几何法、参数法等,这里使用的是直接法,直接法的步骤是:建系、设点、列式、坐标化、化简整理、最后是多退少补,特别要注意多退少补.
试题解析:(1)由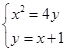 ,消去
,消去 整理得:
整理得: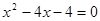 2分
2分
设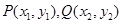 ,则
,则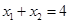 ,
,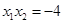
所以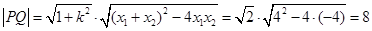 6分
6分
(注:用其他方法也相应给分)
(2)设点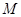 的坐标为
的坐标为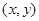 ,由
,由 边所在的方程过定点
边所在的方程过定点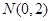 ,
,
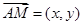
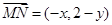 8分
8分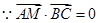
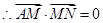
所以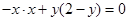 , 即
, 即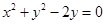 (
(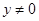 ) 14分
) 14分
(注:没写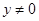 扣1分)
扣1分)
考点:1.直线与抛物线;2.求轨迹方程.

练习册系列答案
相关题目
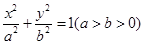 的离心率为
的离心率为  ,且过点
,且过点 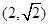
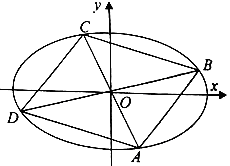
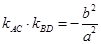 .
.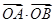 的最值:
的最值: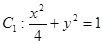 和动圆
和动圆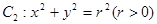 ,直线:
,直线: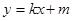 与
与 和
和 分别有唯一的公共点
分别有唯一的公共点 .
. 的取值范围;
的取值范围;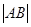 的最大值,并求此时圆
的最大值,并求此时圆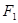 和
和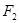 ,且|
,且|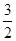 )在该椭圆上.
)在该椭圆上. 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若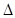 A
A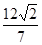 ,求以
,求以
 和直线L:
和直线L: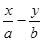 ="1," 椭圆的离心率
="1," 椭圆的离心率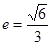 ,坐标原点到直线L的距离为
,坐标原点到直线L的距离为 。
。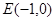 ,若直线
,若直线
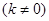 与椭圆C相交于M、N两点,试判断是否存在
与椭圆C相交于M、N两点,试判断是否存在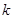 值,使以MN为直径的圆过定点E?若存在求出这个
值,使以MN为直径的圆过定点E?若存在求出这个 ,直线l过定点
,直线l过定点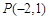 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?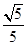 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.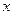 轴上的椭圆的离心率为
轴上的椭圆的离心率为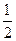 ,它的长轴长等于圆
,它的长轴长等于圆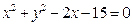 的半径,则椭圆的标准方程是
的半径,则椭圆的标准方程是 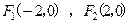 ,则这个椭圆的离心率等于_________________:
,则这个椭圆的离心率等于_________________: