题目内容
已知椭圆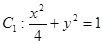 和动圆
和动圆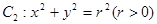 ,直线:
,直线: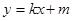 与
与 和
和 分别有唯一的公共点
分别有唯一的公共点 和
和 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)求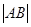 的最大值,并求此时圆
的最大值,并求此时圆 的方程.
的方程.
(Ⅰ)[1,2)(Ⅱ)1,x2+y2=2
解析试题分析:(Ⅰ)将直线 方程与椭圆方程联立消去
方程与椭圆方程联立消去 整理成关于
整理成关于 的一元二次方程,因为直线与椭圆只有一个公共点,则判别式为0,列出关于m,k的方程,再由直线
的一元二次方程,因为直线与椭圆只有一个公共点,则判别式为0,列出关于m,k的方程,再由直线 与圆只有一个公共点知,直线
与圆只有一个公共点知,直线 与圆相切,利用圆心到直线的距离等于半径找出r,m,k关系,将这两个关于m,k的方程联立,消去m,将r表示成k的函数,利用函数求值域的方法,求出r范围;(Ⅱ)由(Ⅰ)可求得A,B两点的横坐标,利用弦长公式将AB用r表示出来,利用函数求最值的方法,求出|AB|的最大值及取最大值时的r值,从而写出圆的方程.
与圆相切,利用圆心到直线的距离等于半径找出r,m,k关系,将这两个关于m,k的方程联立,消去m,将r表示成k的函数,利用函数求值域的方法,求出r范围;(Ⅱ)由(Ⅰ)可求得A,B两点的横坐标,利用弦长公式将AB用r表示出来,利用函数求最值的方法,求出|AB|的最大值及取最大值时的r值,从而写出圆的方程.
试题解析:(Ⅰ)由
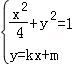 ,得(1+4k2)x2+8kmx+4(m2﹣1)=0.
,得(1+4k2)x2+8kmx+4(m2﹣1)=0.
由于l与C1有唯一的公共点A,故△1=64k2m2﹣16(1+4k2)(m2﹣1)=0, 2分
从而m2=1+4k2 ①
由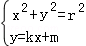 ,得(1+k2)x2+2kmx+m2﹣r2=0.
,得(1+k2)x2+2kmx+m2﹣r2=0.
由于l与C2有唯一的公共点B,故△2=4k2m2﹣4(1+k2)(m2﹣r2)=0, 4分
从而m2=r2(1+k2) ②
由①、②得k2=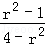 .
.
由k2≥0,得1≤r2<4,所以r的取值范围是[1,2). 6分
(Ⅱ)设A(x1,y1),B(x2,y2),由(Ⅰ)的解答可知
x1=﹣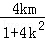 =﹣
=﹣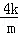 ,x2=﹣
,x2=﹣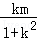 =﹣
=﹣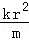 .
.
|AB|2=(1+k2)(x2﹣x1)2=(1+k2)•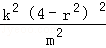 =
=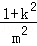 •k2•(4﹣r2)2
•k2•(4﹣r2)2
=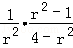 •(4﹣r2)2=
•(4﹣r2)2=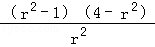 , 9分
, 9分
所以|AB|2=5﹣(r2+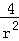 )(1≤r<2).
)(1≤r<2).
因为r2+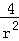 ≥2×2=4,当且仅当r=
≥2×2=4,当且仅当r=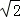 时取等号,
时取等号,
所以当r=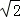 时,|AB|取最大值1,此时C2的方程为x2+y2=2. 12分
时,|AB|取最大值1,此时C2的方程为x2+y2=2. 12分
考点:直线与椭圆的位置关系,直线与圆的位置关系,最值问题,转化与化归思想,运算求解能力

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案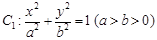 的离心率为
的离心率为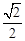 ,
,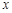 轴被曲线
轴被曲线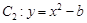 截得的线段长等于
截得的线段长等于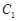 的短轴长.
的短轴长.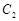 与
与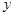 轴的交点为
轴的交点为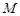 ,过坐标原点
,过坐标原点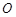 的直线
的直线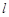 与
与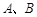 ,直线
,直线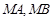 分别与
分别与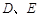 .
.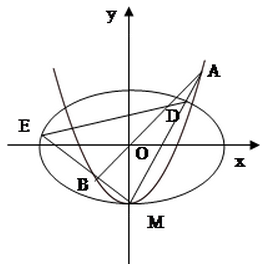
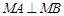 ;
;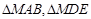 的面积分别为
的面积分别为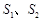 ,若
,若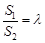 ,求
,求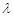 的取值范围.
的取值范围.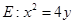 .
.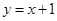 与抛物线
与抛物线 相交于
相交于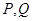 两点,求
两点,求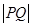 弦长;
弦长; 的三个顶点在抛物线
的三个顶点在抛物线 边过定点
边过定点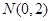 ,点
,点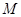 在
在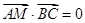 ,求点
,求点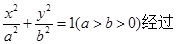 点
点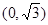 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为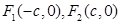
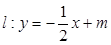 与椭圆交于
与椭圆交于 两点,与以
两点,与以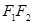 为直径的圆交于
为直径的圆交于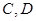 两点,且满足
两点,且满足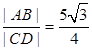 ,求直线
,求直线 的方程.
的方程.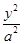 +
+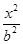 =1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(
=1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(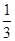 ,
,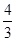 ).
).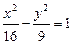 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是 .
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是 .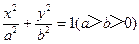 的左、右焦点分别是F1,F2,过F2作倾斜角为
的左、右焦点分别是F1,F2,过F2作倾斜角为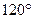 的直线与椭圆的一个交点为M,若MF1垂直于x轴,则椭圆的离心率为______
的直线与椭圆的一个交点为M,若MF1垂直于x轴,则椭圆的离心率为______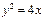 上有两点A、B,且|AB|=6.则线段AB的中点M到y轴的最小距离为 .
上有两点A、B,且|AB|=6.则线段AB的中点M到y轴的最小距离为 .