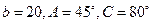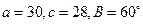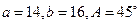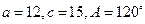题目内容
(本小题满分12分)如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=20km,BC=10km.为了处理这三家工厂的污水,现要在该矩形区域上(含边界)且与A,B等距的一点O处,建造一个污水处理厂,并铺设三条排污管道AO,BO,PO.记铺设管道的总长度为ykm.
(1)按下列要求建立函数关系式:
(i)设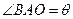 (rad),将
(rad),将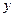 表示成
表示成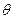 的函数;
的函数;
(ii)设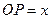 (km),将
(km),将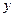 表示成
表示成 的函数;
的函数;
(2)请你选用(1)中的一个函数关系确定污水处理厂的位置,使铺设的污水管道的总长度最短。
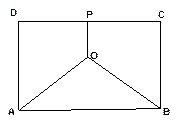
(1)按下列要求建立函数关系式:

(i)设
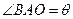 (rad),将
(rad),将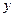 表示成
表示成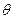 的函数;
的函数;(ii)设
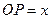 (km),将
(km),将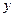 表示成
表示成 的函数;
的函数;(2)请你选用(1)中的一个函数关系确定污水处理厂的位置,使铺设的污水管道的总长度最短。
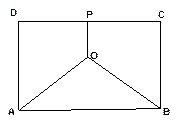
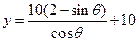

 ;
;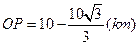 时,管道总长度最短
时,管道总长度最短(1) (i)由条件知PQ 垂直平分AB,若∠BAO=
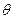 (rad) ,
(rad) ,则
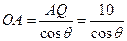 ,
,
故
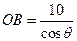 ,OP=
,OP=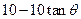 , 。。。。。。。。。。。(2分)
, 。。。。。。。。。。。(2分)所以
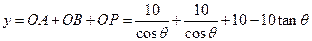 ,
,所求函数关系式为
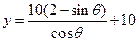
 ①。。。。。。。(4分
①。。。。。。。(4分

 )
)(没注明定义域扣1分)
(ii)若OP=
 (km) ,则OQ=10-
(km) ,则OQ=10- ,所以OA
,所以OA =OB=
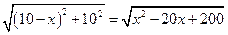 。。。。。。。。。。。。。。。。。。(6分)
。。。。。。。。。。。。。。。。。。(6分)所求函数关系式为
 。。。。。。。。。(8分)
。。。。。。。。。(8分)(没注明定义域扣1分)
(2)若选择函数模型①,设
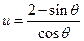
则

解得
 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。(10分)
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。(10分)


当
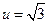 时,
时,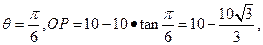
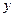 取得最小值.
取得最小值.故当
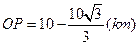 时,管道总长度最短.。。。。。。。。。。。。。。。。。(12分)
时,管道总长度最短.。。。。。。。。。。。。。。。。。(12分)若选择函数模型

平方化简得

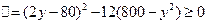
解得
 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。(10分)
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。(10分)将
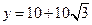 代入方程,得
代入方程,得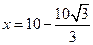
故当
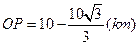 时,管道总长度最短. 。。。。。。。。。。。。。。。。(12分)
时,管道总长度最短. 。。。。。。。。。。。。。。。。(12分)



练习册系列答案
相关题目
 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;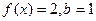 ,△ABC的面积为
,△ABC的面积为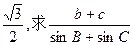 的值。
的值。 海里,且在北偏东
海里,且在北偏东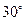 方向;测得灯塔B与A相距
方向;测得灯塔B与A相距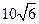 海里,且在北偏西
海里,且在北偏西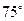 方向,船由A向正北方向航行到C处,测得灯塔B在南偏西
方向,船由A向正北方向航行到C处,测得灯塔B在南偏西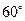 方向,这时灯塔D与C相距多少海里?D在C的什么方向?
方向,这时灯塔D与C相距多少海里?D在C的什么方向?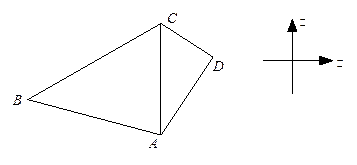
 中,
中,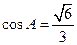 ,
,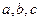 分别是角
分别是角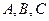 所对的边.
所对的边.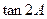 ;
;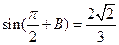 ,
,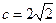 ,求
,求 .
. 方向,距离A为
方向,距离A为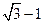
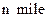 的B处有一艘走私船,在A处北偏西
的B处有一艘走私船,在A处北偏西 方向,距离A为
方向,距离A为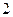
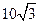
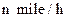 的速度追截走私船,此时,走私船正以
的速度追截走私船,此时,走私船正以
 方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便) 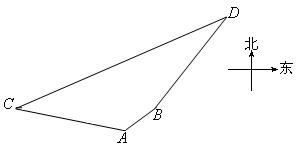
 的正三角形ABC中,设
的正三角形ABC中,设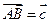 ,
, 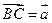 ,
, 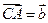 .则
.则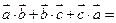 ( )
( )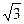 ,则边c的值为 ▲ .
,则边c的值为 ▲ .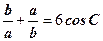 ,则
,则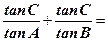 __
__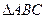 ,由已知条件解三角形,其中有两解的是 ( )
,由已知条件解三角形,其中有两解的是 ( )