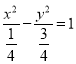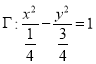题目内容
【题目】我们称一个非负整数集合![]() (非空)为好集合,若对任意
(非空)为好集合,若对任意![]() ,或者
,或者![]() ,或者
,或者![]() .以下记
.以下记![]() 为
为![]() 的元素个数.
的元素个数.
(Ⅰ)给出所有的元素均小于![]() 的好集合;(给出结论即可)
的好集合;(给出结论即可)
(Ⅱ)求出所有满足![]() 的好集合;(同时说明理由)
的好集合;(同时说明理由)
(Ⅲ)若好集合![]() 满足
满足![]() ,求证:
,求证: ![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均为
中所有元素均为![]() 的整数倍.
的整数倍.
【答案】(Ⅰ)![]() .(Ⅱ)见解析;.(Ⅲ)见解析.
.(Ⅱ)见解析;.(Ⅲ)见解析.
【解析】试题分析:(1)根据题意得到集合为![]() ;(2)设
;(2)设![]() ,其中
,其中![]() ,则由题意:
,则由题意: ![]() ,故
,故![]() ,即
,即![]() ,根据题干中的条件限制元素特性,进而找到满足条件的好集合;(3)通过归纳可得到结果.
,根据题干中的条件限制元素特性,进而找到满足条件的好集合;(3)通过归纳可得到结果.
解析:
(Ⅰ)![]() .
.
(Ⅱ)设![]() ,其中
,其中![]() ,则由题意:
,则由题意: ![]() ,故
,故![]() ,即
,即![]() .
.
考虑![]() ,可知
,可知![]() ,所以
,所以![]() 或
或![]() .
.
若![]() ,则考虑
,则考虑![]() ,由于
,由于![]() ,所以
,所以![]() ,因此
,因此![]() .
.
所以![]() .但此时考虑
.但此时考虑![]() ,但
,但![]() ,不满足题意.
,不满足题意.
若![]() ,此时
,此时![]() 满足题意.
满足题意.
所以![]() ,其中
,其中![]() 为相异正整数.
为相异正整数.
(Ⅲ)记![]() ,则
,则![]() .
.
首先, ![]() .设
.设![]() ,其中
,其中![]() .
.
分别考虑![]() 和其他任一元素
和其他任一元素![]() ,由题意可得
,由题意可得![]() 也在
也在![]() 中.
中.
而![]() ,
,
所以![]() ,所以
,所以![]() .
.
对于![]() ,考虑
,考虑![]() ,其和大于
,其和大于![]() ,故其差
,故其差![]() .
.
特别的, ![]() ,所以
,所以![]() .
.
由![]() ,且
,且![]() ,所以
,所以![]() ,
,
通过归纳可得: ![]() .
.
所以![]() ,此时
,此时![]() .得证.
.得证.

练习册系列答案
相关题目