题目内容
【题目】点![]() 是函数
是函数![]() 的图象的一个对称中心,且点
的图象的一个对称中心,且点![]() 到该图象的对称轴的距离的最小值为
到该图象的对称轴的距离的最小值为![]() .
.
①![]() 的最小正周期是
的最小正周期是![]() ;
;
②![]() 的值域为
的值域为![]() ;
;
③![]() 的初相
的初相![]() 为
为![]() ;
;
④![]() 在
在![]() 上单调递增.
上单调递增.
以上说法正确的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由条件利用正弦函数的周期性、单调性、最值,以及图象的对称性,即可得出结论.
∵点P(﹣![]() ,1)是函数f(x)=sin(ωx+φ)+m(ω>0,|φ|<
,1)是函数f(x)=sin(ωx+φ)+m(ω>0,|φ|<![]() )的图象的一个对称中心,∴m=1,ω(﹣
)的图象的一个对称中心,∴m=1,ω(﹣![]() )+φ=kπ,k∈Z.
)+φ=kπ,k∈Z.
∵点P到该图象的对称轴的距离的最小值为![]() ,∴ω=2,
,∴ω=2,
∴φ=kπ+![]() , k∈Z,又|φ|<
, k∈Z,又|φ|<![]() ∴φ=
∴φ=![]() ,f(x)=sin(2x+
,f(x)=sin(2x+![]() )+1.
)+1.
故①f(x)的最小正周期是π,正确;②f(x)的值域为[0,2],正确;
③f(x)的初相φ为![]() ,正确;
,正确;
④在[![]() ,2π]上,2x+
,2π]上,2x+![]() ∈[
∈[![]() ,
,![]() ],根据函数的周期性,函数单调性与 [﹣
],根据函数的周期性,函数单调性与 [﹣![]() ,
,![]() ]时的单调性相同,故函数f(x)单调递增,故④正确,
]时的单调性相同,故函数f(x)单调递增,故④正确,
故选:D.

练习册系列答案
相关题目
【题目】某银行对某市最近5年住房贷款发放情况(按每年6月份与前一年6月份为1年统计)作了统计调查,得到如下数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
贷款 | 50 | 60 | 70 | 80 | 100 |
(1)将上表进行如下处理:![]() ,
,
得到数据:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
试求![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,再写出
,再写出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() .
.
(2)利用(1)中所求的线性回归方程估算2019年房贷发放数额.
参考公式: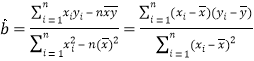 ,
, ![]()
