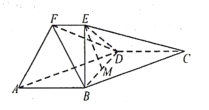
题目内容
【题目】已知椭圆C1:![]() (a>b>0)与双曲线 C2:x2﹣
(a>b>0)与双曲线 C2:x2﹣![]() 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点,若C1恰好将线段AB三等分,则椭圆C1的离心率为 ( )
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点,若C1恰好将线段AB三等分,则椭圆C1的离心率为 ( )
A. e2=![]() B. e2=
B. e2=![]() C. e2=
C. e2=![]() D. e2=
D. e2=![]()
【答案】A
【解析】
根据双曲线方程,确定一条渐近线为y=2x,可得AB=2a且AB为题中圆的直径.由椭圆与双曲线有公共焦点,可得a2﹣b2=5.设C1与y=2x在第一象限的交点为C(m,2m),代入C1解出m2=![]() .再由对称性知直线y=2x被C1截得的弦长CD=2
.再由对称性知直线y=2x被C1截得的弦长CD=2![]() m,根据C1恰好将线段AB三等分解出m=
m,根据C1恰好将线段AB三等分解出m=![]() ,联解可得a2、b2、c2的值,结合离心率的公式加以计算,可得答案.
,联解可得a2、b2、c2的值,结合离心率的公式加以计算,可得答案.

由题意,C2的焦点为(±![]() ,0),一条渐近线方程为y=2x,
,0),一条渐近线方程为y=2x,
根据对称性可知以C1的长轴为直径的圆交y=2x于A、B两点,满足AB为圆的直径且AB=2a
∵椭圆C1与双曲线C2有公共的焦点,
∴C1的半焦距c=![]() ,可得a2﹣b2=5,…①
,可得a2﹣b2=5,…①
设C1与y=2x在第一象限的交点的坐标为C(m,2m),
代入C1的方程,解得m2=![]() ,…②
,…②
由对称性可得直线y=2x被C1截得的弦长CD=2![]() m,
m,
结合题意得2![]() m=
m=![]() ,可得m=
,可得m=![]() ,…③
,…③
由②③联解,得a2=11b2…④
再联解①④,可得a2=5.5,b2=0.5,得c2=a2﹣b2=5.
∴椭圆C1的离心率e满足e2=![]() =
=![]() .
.
故选:A.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.