题目内容
设f(x)定义域为D,若满足:
(1)f(x)在D内是单调函数;
(2)存在[a,b]⊆D,使f(x)在x∈[a,b]时值域也为[a,b],则称f(x)为D上的闭函数.
当f(x)=2k+
时,k的取值范围是 .
(1)f(x)在D内是单调函数;
(2)存在[a,b]⊆D,使f(x)在x∈[a,b]时值域也为[a,b],则称f(x)为D上的闭函数.
当f(x)=2k+
| x+4 |
考点:函数单调性的性质
专题:计算题,新定义,函数的性质及应用
分析:由已知中闭函数的定义,及函数f(x)的解析式,我们可得函数满足条件(1),即在定义域D内是单调函数,若满足条件(2)则f(x)=x在区间[-4,+∞)上有两个根,利用换元法,可将条件转化为t2-t-(4+2k)=0有两个非负根,结合二次方程根与系数的关系,可得关于k的不等式组,进而求出k的范围.
解答:
解:∵f(x)=2k+
在定义域D=[-4,+∞)上为增函数,
故满足条件(1)
若存在[a,b]⊆D使f(x)在x∈[a,b]值域为[a,b],
则f(x)=2k+
=x在区间[-4,+∞)上有两个根,
令t=
(t≥0)
则原方程可化为t2-t-(4+2k)=0有两个非负根,
即
,
解得-
<k≤-
,
故k的范围是(-
,-
].
故答案为:(-
,-
].
| x+4 |
故满足条件(1)
若存在[a,b]⊆D使f(x)在x∈[a,b]值域为[a,b],
则f(x)=2k+
| x+4 |
令t=
| x+4 |
则原方程可化为t2-t-(4+2k)=0有两个非负根,
即
|
解得-
| 17 |
| 8 |
| 1 |
| 2 |
故k的范围是(-
| 17 |
| 8 |
| 1 |
| 2 |
故答案为:(-
| 17 |
| 8 |
| 1 |
| 2 |
点评:本题考查的知识点是单调性的性质,其中正确理解新定义“闭函数”中的两个条件的意义,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若数列{an}满足
-
=d(n∈Nn,d为常数),则称数列{an}为“调和数列”.已知数列{
}为“调和数列”,且x1+x2+…+x20=200,则x3•x18的最大值为( )
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| xn |
| A、50 | B、100 |
| C、150 | D、200 |
给出下列四个命题:
①若直线a∥平面α,直线b⊥α,则a⊥b;
②若直线a∥平面α,α⊥平面β,则a⊥β;
③若a、b是二条平行直线,b?平面α,则a∥α;
④若平面α⊥平面β,平面γ⊥β,则α∥γ.
其中不正确的命题的个数是( )
①若直线a∥平面α,直线b⊥α,则a⊥b;
②若直线a∥平面α,α⊥平面β,则a⊥β;
③若a、b是二条平行直线,b?平面α,则a∥α;
④若平面α⊥平面β,平面γ⊥β,则α∥γ.
其中不正确的命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
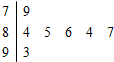 如图是2012年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
如图是2012年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A、85,84 |
| B、84,84 |
| C、84,85 |
| D、85,85 |
设有直线a,b,c,d及平面α,β,下列条件能推出α∥β的是( )
| A、a?α,b?β,a∥b,c?α,d?β,c∥d |
| B、a?α,b?β,a∥β,b∥α |
| C、a⊥α,b⊥β,a∥b |
| D、平面α内有三个不共线的点到β距离相等 |
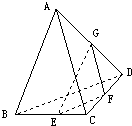 E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )
E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )