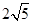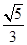题目内容
如图,在三棱锥S﹣ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )
A. | B. | C. | D. |
D
解析试题分析:由题意得,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角即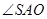 ;该三棱锥是正三棱锥,
;该三棱锥是正三棱锥, 在底面上的射影
在底面上的射影 是
是 的中心,也是重心,由重心定理得
的中心,也是重心,由重心定理得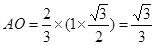 ,又因为
,又因为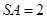 ,所以
,所以 ,即侧棱SA与底面ABC所成角的余弦值为
,即侧棱SA与底面ABC所成角的余弦值为 .
.
考点:直线与平面所成的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
M.N分别为正方体中棱BC和棱CC1的中点,则异面直线AC和MN所成的角为 ( )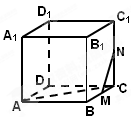
| A.30° | B.45° | C.60° | D.90° |
直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,则
,则 与
与 所成的角的余弦值为( ).
所成的角的余弦值为( ).
A. | B. | C. | D. |
对于平面α和共面的直线m、n,下列命题正确的是( )
| A.若m、n与α所成的角相等,则m∥n |
| B.若m∥α,n∥α,则m∥n |
| C.若m⊥α,m⊥n,则n∥α |
D.若m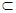 α,n∥α,则m∥n α,n∥α,则m∥n |
 的正三角形,俯视图轮廓为正方形,试描述该几何体的特征,并求该几何体的体积和表面积.
的正三角形,俯视图轮廓为正方形,试描述该几何体的特征,并求该几何体的体积和表面积.
 ,
, 时,求二面角A—EF—C的大小.
时,求二面角A—EF—C的大小.
 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E ∥平面
∥平面 ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m 

 的余弦值
的余弦值