题目内容
14. 如图,在四棱锥P-ABCD中,底面ABCD为梯形,∠ABC=∠BAD=90°,AP=AD=AB=$\sqrt{2}$,BC=t,∠PAB=∠PAD=α.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,∠ABC=∠BAD=90°,AP=AD=AB=$\sqrt{2}$,BC=t,∠PAB=∠PAD=α.(Ⅰ)当t=3$\sqrt{2}$时,试在棱PA上确定一个点E,使得PC∥平面BDE,并求出此时$\frac{AE}{EP}$的值;
(Ⅱ)当α=60°时,若平面PAB⊥平面PCD,求此时棱BC的长.
分析 (Ⅰ)在棱PA上取点E,使得$\frac{AE}{EP}$=$\frac{1}{3}$,连接AC,BD交于点F,证明EF∥PC,即可证明PC∥平面BDE;
(Ⅱ)取BC上一点G使得BG=$\sqrt{2}$,连结DG,则ABGD为正方形.过P作PO⊥平面ABCD,垂足为O.连结OA,OB,OD,OG,以O坐标原点,分别以$\overrightarrow{OG},\overrightarrow{OB},\overrightarrow{OP}$的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,求出平面PAB的法向量$\overrightarrow{m}$=(-1,1,1)、同平面PCD的法向量$\overrightarrow{n}$=(1-$\frac{2\sqrt{2}}{t}$,1,-1),由$\overrightarrow{m}•\overrightarrow{n}$=0,解得BC的长.
解答  解:(1)在棱PA上取点E,使得$\frac{AE}{EP}$=$\frac{1}{3}$,-------2
解:(1)在棱PA上取点E,使得$\frac{AE}{EP}$=$\frac{1}{3}$,-------2
连接AC,BD交于点F,
因为AD∥BC,
所以$\frac{AF}{FC}=\frac{AD}{BC}$=$\frac{1}{3}$,
所以$\frac{AE}{EP}$=$\frac{AF}{AC}$,所以,EF∥PC
因为PC?平面BDE,EF?平面BDE
所以PC∥平面BDE-------------4
(Ⅱ)取BC上一点G使得BG=$\sqrt{2}$,连结DG,则ABGD为正方形.过P作PO⊥平面ABCD,垂足为O.连结OA,OB,OD,OG.
AP=AD=AB,∠PAB=∠PAD=60°,
所以△PAB和△PAD都是等边三角形,因此PA=PB=PD,
所以OA=OB=OD,
即点O为正方形ABGD对角线的交点,---------------7
以O坐标原点,分别以$\overrightarrow{OG},\overrightarrow{OB},\overrightarrow{OP}$的方向为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系O-xyz.
则O(0,0,0),P(0,0,1),A(-1,0,0),B(0,1,0),D(0,-1,0),G(1,0,0)
设棱BC的长为t,则C($\frac{\sqrt{2}}{2}$t,1-$\frac{\sqrt{2}}{2}$t,0),
$\overrightarrow{PA}$=(-1,0,-1),$\overrightarrow{PB}$=(0,1,-1),$\overrightarrow{PC}$=($\frac{\sqrt{2}}{2}$t,1-$\frac{\sqrt{2}}{2}$t,-1),$\overrightarrow{PD}$=(0,-1,-1)--------------9
设平面PAB的法向量为$\overrightarrow{m}$=(x,y,z),则
$\left\{\begin{array}{l}{-x-z=0}\\{y-z=0}\end{array}\right.$,取$\overrightarrow{m}$=(-1,1,1)-----------10
同理平面PCD的法向量$\overrightarrow{n}$=(1-$\frac{2\sqrt{2}}{t}$,1,-1)-----------11
由$\overrightarrow{m}•\overrightarrow{n}$=0,解得t=2$\sqrt{2}$,即BC的长为2$\sqrt{2}$----------------12
点评 本题主要考查了线面平行的判定定理及性质,考查向量方法的运用,正确建立坐标系,求出平面的法向量是关键.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
| A. | 1 | B. | i | C. | -i | D. | -1 |
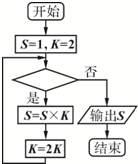
| A. | k<32? | B. | k<63? | C. | k<64? | D. | k<70? |
 已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积等于$\frac{8}{3}$,全面积为2(3+$\sqrt{2}$+$\sqrt{5}$).
已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积等于$\frac{8}{3}$,全面积为2(3+$\sqrt{2}$+$\sqrt{5}$).