题目内容
(本小题共14分)
已知点![]() 为圆
为圆![]() 上的动点,且
上的动点,且![]() 不在
不在![]() 轴上,
轴上,![]() 轴,垂足为
轴,垂足为![]() ,线段
,线段![]() 中点
中点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过定点
,过定点![]()
![]() 任作一条与
任作一条与![]() 轴不垂直的直线
轴不垂直的直线![]() ,它与曲线
,它与曲线![]() 交于
交于![]() 、
、![]() 两点。
两点。
(1)求曲线![]() 的方程;
的方程;
(2)试证明:在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 总能被
总能被![]() 轴平分
轴平分
(1)设![]() 为曲线
为曲线![]() 上的任意一点,则点
上的任意一点,则点![]() 在圆
在圆![]() 上,
上,
∴![]() ,曲线
,曲线![]() 的方程为
的方程为![]() . ………………2分
. ………………2分
(2)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() , ………………3分
, ………………3分
代入曲线![]() 的方程
的方程![]() ,可得
,可得
![]() , ………………5分
, ………………5分
∵![]() ,∴
,∴![]() ,
,
∴直线![]() 与曲线
与曲线![]() 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆![]() 的内部得到此结论)
的内部得到此结论)
………………6分
设点![]() ,
,![]() 的坐标分别
的坐标分别![]() ,
, ![]() ,
,
则![]() ,
,
要使![]() 被
被![]() 轴平分,只要
轴平分,只要![]() , ………………9分
, ………………9分
即![]() ,
,![]() , ………………10分
, ………………10分
也就是![]() ,
,![]() ,
,
即![]() ,即只要
,即只要![]() ………………12分
………………12分
当![]() 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而![]() 总能被
总能被![]() 轴平分.
轴平分.
………………13分
所以在x轴上存在定点![]() ,使得
,使得![]() 总能被
总能被![]() 轴平分.
轴平分.
………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是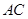 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.