题目内容

20．化简5${\;}^{lo{g}_{25}}$${\;}^{（l{g}^{2}2+l{g}^{\frac{5}{2}}}）$的结果是（　　）
A．lg$\frac{1}{5}$B．lg5C．lg2$\frac{1}{5}$D．lg25

分析 根据对数的运算性质即可求出．

解答 解：lg22+lg$\frac{5}{2}$=lg22+lg5-lg2=lg2（lg2-1）+lg5=lg2lg$\frac{1}{5}$+lg5=lg5（1-lg2）=lg5lg5=lg25，
∴5${\;}^{lo{g}_{25}}$${\;}^{（l{g}^{2}2+l{g}^{\frac{5}{2}}}）$=${5}^{lo{{g}_{25}}^{l{g}^{2}5}}$=${5}^{lo{g}_{5}lg5}$=lg5，
故选：B．

点评 本题考查了对数的运算性质，属于基础题．

练习册系列答案
相关题目
10．给出下列命题：
①若“p或q”是假命题，则“?p且?q”是真命题；
②若实系数关于x的二次不等式，ax2+bx+c≤0的解集为∅，则必有a＞0且△≤0；
③|x|＞|y|?x2＞y2；
④$\left\{\begin{array}{l}x＞2\\ y＞2\end{array}\right.?\left\{\begin{array}{l}x+y＞4\\ xy＞4\end{array}\right.$．
其中真命题的是①③．（填写序号）
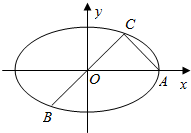11．如图所示，已知A、B、C是长轴为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且AC⊥BC，|BC|=2|AC|．
（1）求椭圆E的方程；
（2）设P为椭圆E上异于其顶点的任一点，以OP为直径的圆与圆x2+y2=$\frac{4}{3}$相交于点M、N，若直线MN在x轴、y轴上的截距分别为m、n，证明：$\frac{1}{3{m}^{2}}$+$\frac{1}{{n}^{2}}$为定值．
8．在△ABC中，角$C=\frac{π}{3}$，边AB=1，则△ABC周长的取值范围是（　　）
A．（2，3]B．[1，3]C．（0，2]D．（2，5]
15．设F1，F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞1）的两个焦点，其离心率为$\frac{\sqrt{3}}{2}$．
（1）设点P为椭圆上任一点，则△PF1F2的周长是否为一定值？请说明理由；
（2）在椭圆上是否存在点M，使得MF1⊥MF2？若存在，求点M的坐标；若不存在，说明理由．
5．求函数f（x）=$\frac{\sqrt{{x}^{2}+x-2}}{|x|-1}$的定义域．
12．已知A={x|x＜-2或x＞5}，B={x|a≤x＜a+2}，若A?B，则实数a的取值范围是a≤-4或a＞5．
9．设集合A={m+n$\sqrt{3}$|m2-3n2=1，m，n∈Z}．
（1）证明：若a∈A，则$\frac{1}{a}$∈A，且$\frac{a}{2+\sqrt{3}}$∈A；
（2）对于实数p，q，如果1＜p≤q，证明：2$＜p+\frac{1}{p}≤q+\frac{1}{q}$；并由此说明，A中元素若满足1$＜b≤2+\sqrt{3}$，则b=2$+\sqrt{3}$；
（3）设c∈A，试求满足2$+\sqrt{3}$＜c≤（2$+\sqrt{3}$）2的A的元素．
10．函数y=（$\frac{2}{3}$）${\;}^{{x}^{2}-2x}$的单调增区间是（-∞，1]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网