题目内容
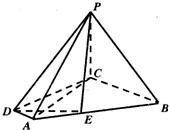 已知四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=
已知四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=| π | 2 |
(I)求证:DE⊥平面PAC;
(II)求二面角B-PA-C的大小.
分析:(I)取CD中点F,连接EF,欲证DE⊥平面PAC,根据直线与平面垂直的判定定理可知只需证DE与平面PAC内两相交直线垂直,而DE⊥AC,PC⊥DE,满足定理条件;
(II)以点C为坐标原点,分别以CD,CB,CP为x轴,y轴,z轴建立空间直角坐标系Oxyz,求出平面PAC的法向量
和平面PAB的一个法向量为
,计算两个法向量的夹角,即可求出二面角B-PA-C的大小.
(II)以点C为坐标原点,分别以CD,CB,CP为x轴,y轴,z轴建立空间直角坐标系Oxyz,求出平面PAC的法向量
| DE |
| n |
解答:解:(I)取CD中点F,连接EF,
则EF⊥CD,EF=
(AD+BC)=2
∵AD=DF=1,CD=EF=2,∠CDA=∠EFD=90°
∴△CDA≌△EFD∴∠DAC=∠FDE
∵∠EDA+∠FDE=90°∴∠EDA+∠DAC=90°∴DE⊥AC(4分)
∵PC⊥平面ABCD,∴PC⊥DE∴DE⊥平面PAC(6分)
(II)以点C为坐标原点,分别以CD,CB,CP为x轴,y轴,z轴建立空间直角坐标系Oxyz,
则C(0,0,0),D(2,0,0),B(0,3,0),P(0,0,2),A(2,1,0),E(1,2,0)
∵DE⊥平面PAC∴平面PAC的一个法向量为
=(-1,2,0)(8分)
设平面PAB的一个法向量为
=(x,y,z),
由
=(2,1,-2),
=(0,3,-2),
得
不妨令x=1,则y=1,z=
,
即
=(1,1,
)(10分)
∴cos<
,
>=
=
∴二面角B-PA-C的大小为arccos
.(12分)
则EF⊥CD,EF=
| 1 |
| 2 |
∵AD=DF=1,CD=EF=2,∠CDA=∠EFD=90°
∴△CDA≌△EFD∴∠DAC=∠FDE
∵∠EDA+∠FDE=90°∴∠EDA+∠DAC=90°∴DE⊥AC(4分)
∵PC⊥平面ABCD,∴PC⊥DE∴DE⊥平面PAC(6分)
(II)以点C为坐标原点,分别以CD,CB,CP为x轴,y轴,z轴建立空间直角坐标系Oxyz,
则C(0,0,0),D(2,0,0),B(0,3,0),P(0,0,2),A(2,1,0),E(1,2,0)
∵DE⊥平面PAC∴平面PAC的一个法向量为
| DE |
设平面PAB的一个法向量为
| n |
由
| PA |
| PB |
得
|
不妨令x=1,则y=1,z=
| 3 |
| 2 |
即
| n |
| 3 |
| 2 |
∴cos<
| DE |
| n |
(-1)•1+2•1+0•
| ||||||
|
2
| ||
| 85 |
∴二面角B-PA-C的大小为arccos
2
| ||
| 85 |
点评:本题主要考查了直线与平面垂直的判定,以及利用空间向量求二面角的大小,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.