题目内容
7.将函数f(x)=$\sqrt{3}sinxcosx+{cos^2}x-\frac{1}{2}$的图象向左平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)是( )| A. | 周期为π的奇函数 | B. | 周期为π的偶函数 | ||
| C. | 周期为2π的奇函数 | D. | 周期为2π的偶函数 |
分析 由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x+$\frac{π}{6}$),可得g(x)=cos2x,由三角函数的图象与性质可得函数g(x)是周期为π的偶函数.
解答 解:∵f(x)=$\sqrt{3}sinxcosx+{cos^2}x-\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x=sin(2x+$\frac{π}{6}$)
∴g(x)=sin[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=sin(2x+$\frac{π}{2}$)=cos2x
∴T=$\frac{2π}{2}$=π,即函数g(x)是周期为π的偶函数.
故选:B.
点评 本题考查三角恒等变换,三角函数的图象与性质、图象变换,属于中等题.

练习册系列答案
相关题目
18.问题:①某地区10000名中小学生,其中高中生2000名,初中生4500名,小学生3500名,现从中抽取容量为200的样本;②从1002件同一生产线生产的产品中抽取20件产品进行质量检查.方法:Ⅰ、随机抽样法Ⅱ、分层抽样法Ⅲ、系统抽样法.其中问题与方法配对较适宜的是( )
| A. | ①Ⅰ,②Ⅱ | B. | ①Ⅲ,②Ⅰ | C. | ①Ⅱ,②Ⅲ | D. | ①Ⅲ,②Ⅱ |
15.下列函数中,既是奇函数又在其定义域上是增函数的是( )
| A. | $y=-\frac{2}{x}$ | B. | y=x3 | C. | y=log2x | D. | y=tanx |
 三棱锥O-ABC中,OA⊥OB,OB⊥OC,OC⊥OA,若OA=OB=a,OC=b,D是该三棱锥外部(不含表面)的一点,给出下列四个命题,
三棱锥O-ABC中,OA⊥OB,OB⊥OC,OC⊥OA,若OA=OB=a,OC=b,D是该三棱锥外部(不含表面)的一点,给出下列四个命题,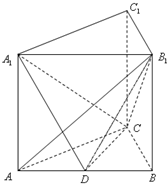 如图、已知直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
如图、已知直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.