Question

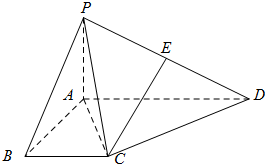如图，四棱锥P-ABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC=∠BAD=90°，AD=2PA=2BC=2
（Ⅰ）求证：平面PAC⊥平面PCD；
（Ⅱ）在线段PD上是否存在点E，使CE与平面PBC所成的角为30⁰？若存在，确定点E的位置；若不存在，说明理由．

Answer 1

分析：（Ⅰ）根据面面垂直的判定定理可证明；
（Ⅱ）以点A为坐标原点，建立坐标系，CE与平面PBC所成的角为30⁰，∴

CE

与平面PBC的法向量

n

=（1，0，1）成60°，利用向量夹角公式可列一方程，解出即可．

解答：证明：（1）连接AC，则AC⊥CD，
又PA⊥平面ABCD，∴PA⊥CD，
∴CD⊥平面PAC，又CD?平面PCD，
∴平面PAC⊥平面PCD．
解：（2）建立坐标系，以点A为坐标原点，

AB

，

AD

，

AP

分别为x、y、z轴正方向，
则B（1，0，0），D（0，2，0），C（1，1，0），P（0，0，1），
∴

DP

=(0，-2，1)，设

DE

=λ 

DP

=(0，-2λ，λ)，
∴

CE

=

CD

+

DE

=(-1，1，0)+(0，-2λ，λ)=(-1，1-2λ，λ)，

BC

=(0，1，0)，

BP

=(1，0，-1)，
设平面PBC的法向量

n

=(x，y，z)，则

y=0 x-z=0

，

n

=（1，0，1），
CE与平面PBC所成的角为30⁰，
∴

CE

与平面PBC的法向量

n

=（1，0，1）成60°．
cos60°=

1

2

=

n •(-1，1-2λ，λ)

| n |• 1+λ2+(1-2λ)2

，得λ=0，即点E的位置为点D，
所以存在点E，与点D重合．

点评：本题考查面面垂直的判定及线面角的求解，向量方法是解决立体几何问题有力的工具．