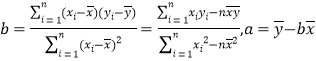题目内容
【题目】函数y=ln（4-x）+1n（2+x）的单调递增区间为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
先求出函数的定义域，利用换元法结合对数函数，一元二次函数的单调性之间的关系进行转化求解即可．
解：要使函数有意义，则
得
得-2＜x＜4，即函数的定义域为（-2，4），
y=ln（4-x）+1n（2+x）=ln（4-x）（2+x）=ln（-x2+2x+8）
设t=-x2+2x+8，则y=lnt为关于t的增函数，
要求函数y=ln（-x2+2x+8）的单调递增区间，
等价为求t=-x2+2x+8的单调递增区间，
∵当-2＜x＜1时，函数t=-x2+2x+8为增函数，
即函数t=-x2+2x+8的单调递增区间为（-2，1），
即函数y=ln（4-x）+1n（2+x）的单调递增区间为（-2，1），
故选：A．
【题目】某校600名文科学生参加了4月25日的三调考试，学校为了了解高三文科学生的数学、外语情况，利用随机数表法从抽取100名学生的成绩进行统计分析，将学生编号为000，001，002，…599
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
（1）若从第6行第7列的数开始右读，请你一次写出最先抽出的5个人的编号（上面是摘自随机数表的第4行到第7行）；
（2）抽出的100名学生的数学、外语成绩如下表：
外语 | ||||
优 | 良 | 及格 | ||
数学 | 优 | 8 | m | 9 |
良 | 9 | n | 11 | |
及格 | 8 | 9 | 11 | |
若数学成绩优秀率为35%，求m，n的值；
（3）在外语成绩为良的学生中，已知m≥12，n≥10，求数学成绩优比良的人数少的概率．
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
（1）请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
;
（2）试根据（1）求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式：
