题目内容
20.已知函数f(x)=$\frac{{x}^{2}+(1+p)x+p}{2x+p}$(p>0),当p>1时,解关于x的不等式f(x)≥0.分析 要解的不等式即 $\frac{(x+p)(x+1)}{2(x+\frac{p}{2})}$≥0,由p>1利用穿根法求得它的解集.
解答 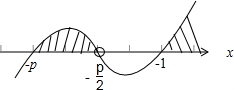 解:关于x的不等式f(x)≥0,即 $\frac{{x}^{2}+(1+p)x+p}{2x+p}$≥0,即 $\frac{(x+p)(x+1)}{2(x+\frac{p}{2})}$≥0,
解:关于x的不等式f(x)≥0,即 $\frac{{x}^{2}+(1+p)x+p}{2x+p}$≥0,即 $\frac{(x+p)(x+1)}{2(x+\frac{p}{2})}$≥0,
由p>1利用穿根法求得它的解集为 {x|-p≤x<-$\frac{p}{2}$,或 x≥-1}.
点评 本题主要考查利用穿根法解分式不等式,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
11.函数y=log2(2x+1)+${(x-2)}^{\frac{1}{2}}$的定义域是( )
| A. | (-∞,2) | B. | (-$\frac{1}{2}$,+∞) | C. | [2,+∞) | D. | (-$\frac{1}{2}$,2) |
12.x是三角形的一个内角,且sinx+cosx=-$\frac{1}{5}$,则tanx的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |