题目内容
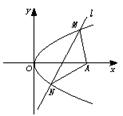
抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为| π | 4 |
分析:根据斜率设出直线l的方程:y=x+b,S=
×|AB|×|y1-y2|,将直线方程与抛物线方程联立,表示出|y1-y2|=
=
=4
,进而求出面积的最大值.
| 1 |
| 2 |
| (y1+y2) 2-4y1y2 |
| 16-16b |
| 1-b |
解答:解:设直线l:y=x+b,直线与x轴交点坐标为B(-b,0),
|AB|=|5+b|,M(x1,y1),N(x2,y2)
联立y=x+b和y2=4x得y2-4y+4b=0
∴|y1-y2|=
=
=4
三角形AMN的最大面积S=
×|AB|×|y1-y2|=2|5+b|×
=2×
[-b3-9b2-15b+25]'=-3b2-18b-15=0,∴b=-1或b=-5(舍)
∴b=-1时,最大面积S=2×
=8
故答案为:8
.
|AB|=|5+b|,M(x1,y1),N(x2,y2)
联立y=x+b和y2=4x得y2-4y+4b=0
∴|y1-y2|=
| (y1+y2) 2-4y1y2 |
| 16-16b |
| 1-b |
三角形AMN的最大面积S=
| 1 |
| 2 |
| 1-b |
| -b3-9b2-15b+25 |
[-b3-9b2-15b+25]'=-3b2-18b-15=0,∴b=-1或b=-5(舍)
∴b=-1时,最大面积S=2×
| -b3-9b2-15b+25 |
| 2 |
故答案为:8
| 2 |
点评:本题考查了抛物线的应用,直线与圆锥曲线联立,利用韦达定理,是圆锥曲线中经常碰到的题型,应该熟练掌握.

练习册系列答案
相关题目
 如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为