题目内容
(2012•梅州二模)设G是一个至少含有两个数的数集,若对任意a,b∈G,都有a+b,a-b,ab,
∈G(除数b≠0),则称G是一个数域,例如有理数集Q是数域.有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数集Q⊆M,则数集M必为数域;④数域必为无限集.其中正确命题的个数是( )
| a |
| b |
分析:利用已知条件中数域的定义判断各命题的真假,题目给出了对两个实数的四种运算,要满足对四种运算的封闭,只有一一验证.
解答:解:因所给数域中的两数a、b完全可以相等,此时a-b=0,
=1,所以①正确;
对于②,取a=1,b=2,则
=
∉G,所以②不正确;
对于③,数集M中多加一个复数i,则1-i∉M,所以③不正确;
因数域中的数可以连续进行四种运算,所以数域必为无限集,所以④正确.
故选B.
| a |
| b |
对于②,取a=1,b=2,则
| a |
| b |
| 1 |
| 2 |
对于③,数集M中多加一个复数i,则1-i∉M,所以③不正确;
因数域中的数可以连续进行四种运算,所以数域必为无限集,所以④正确.
故选B.
点评:本题考查学生对新定义题型的理解和把握能力,理解数域的定义是解决该题的关键,题目着重考查学生的构造性思维,一定要读懂题目再入手,没有一个条件是多余的.

练习册系列答案
相关题目
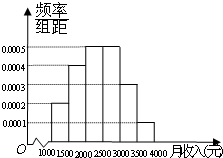 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).