题目内容
20.设函数f(x)=sinx-cosx-ax(0<x<π,常数a∈R),且f(x)同时存在极大值点和极小值点.(1)求a的取值范围;
(2)记f(x)的极大值为M,设实数b,若?λ∈[b+1,b+e](e是自然对数的底数)且?μ∈[b+1,b+e],使得λ+ln(λ-b)<M<μ+ln(μ-b),求实数b的最大值和最小值.
分析 (1)先求导,f(x)同时存在极大值点和极小值点?f′(x)=0在(0,π)内有两根,分别画出y=$\sqrt{2}$sin(x+$\frac{π}{4}$)和y=a的图象,由图象可知a的范围;
(2)由f'(x)=0求得x1,x2,求出函数f(x)的极大值为M,根据?μ∈[b+1,b+e],使得λ+ln(λ-b)<M<μ+ln(μ-b),构造g(x)=x+ln(x-b),x∈[b+1,b+e],利用导数求出M的范围,经过计算比较得到b的范围.
解答 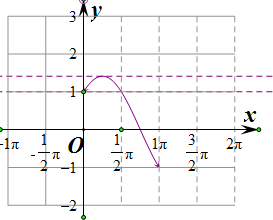 解:(1)∵f(x)=sinx-cosx-ax,
解:(1)∵f(x)=sinx-cosx-ax,
∴f′(x)=cosx+sinx-a=$\sqrt{2}$sin(x+$\frac{π}{4}$)-a,
f(x)同时存在极大值点和极小值点?f′(x)=0在(0,π)内有两根,①
分别画出y=$\sqrt{2}$sin(x+$\frac{π}{4}$)和y=a的图象,如图所示,
由图象可知a的取值范围(1,$\sqrt{2}$)
(2)由f'(x)=0得
x1=arcsin($\frac{a}{\sqrt{2}}$)-$\frac{π}{4}$,x2=$\frac{3π}{4}$-arcsin($\frac{a}{\sqrt{2}}$),
∵f(x)=-$\sqrt{2}$cos(x+$\frac{π}{4}$)-ax,x1∈(0,$\frac{π}{4}$),x2∈($\frac{π}{4}$,$\frac{π}{2}$),
a→1时x1→0,x2→$\frac{π}{2}$,f(x1)→-1,f(x2)→1-$\frac{π}{2}$,
∴f(x1)<f(x2),
∴M=f(x2)=$\sqrt{2-{a}^{2}}$-a($\frac{3π}{4}$-arcsin$\frac{a}{\sqrt{2}}$),
M(1)=1-$\frac{π}{2}$,M($\sqrt{2}$)=-$\frac{\sqrt{2}}{4}π$,
设实数b,若存在λ,μ∈[b+1,b+e]使得λ+ln(λ-b)<M<μ+ln(μ-b),②
设g(x)=x+ln(x-b),x∈[b+1,b+e],
则g'(x)=1+$\frac{1}{x-b}$>0,g(x)是增函数,
由②得b+1<M<b+e+1,
∴b+1≤1-$\frac{π}{2}$≤b+e+1,且b+1≤-$\frac{\sqrt{2}}{4}π$≤b+e+1,
∴-$\frac{π}{2}$-e≤b≤-$\frac{π}{2}$,且-$\frac{\sqrt{2}}{4}π$-e-1≤b≤-$\frac{\sqrt{2}}{4}π$-1,
∴-$\frac{π}{2}$-e≤b≤-$\frac{\sqrt{2}}{4}π$-1,
∴实数b的最大值为-$\frac{\sqrt{2}}{4}π$-1,最小值为-$\frac{π}{2}$-e.
点评 本题考查了导数和函数极值和最值的关系,培养了学生转化能力,运算能力,数形结合的能力,属于难题.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案| A. | a<-$\frac{1}{e}$ | B. | a>-$\frac{1}{e}$ | C. | a<-$\frac{1}{2}$ | D. | a>-$\frac{1}{2}$ |
| A. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处就没有切线 | |
| B. | 若曲线y=f(x)在点(x0,y0)处有切线,则f′(x0)必存在 | |
| C. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处的切线斜率不存在 | |
| D. | 若曲线y=f(x)在点(x0,y0)处没有切线,则f′(x0)有可能存在 |
 如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5,则弦AB的长为$\frac{10}{3}$.
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5,则弦AB的长为$\frac{10}{3}$.