题目内容
已知函数f(x)=xex,其中x∈R.
(Ⅰ)求曲线f(x)在点(x0,x0ex0)处的切线方程
(Ⅱ)如果过点(a,b)可作曲线y=f(x)的三条切线
(1)当-2<a<0时,证明:-
(a+4)<b<f(a);
(2)当a<-2时,写出b的取值范围(不需要书写推证过程).
(Ⅰ)求曲线f(x)在点(x0,x0ex0)处的切线方程
(Ⅱ)如果过点(a,b)可作曲线y=f(x)的三条切线
(1)当-2<a<0时,证明:-
| 1 |
| e2 |
(2)当a<-2时,写出b的取值范围(不需要书写推证过程).
(Ⅰ)∵f(x)=xex,
∴f′(x)=(x+1)ex,
∴曲线f(x)在点(x0,x0ex0)处的切线的斜率k=f′(x0)=(x0+1)ex0,
由点斜式写出切线方程为y-x0ex0=(x0+1)ex0(x-x0),即y=(x0+1)ex0x-x02ex0.
(Ⅱ)(1)如果切线过点(a,b),则存在x0,使b=(x0+1)ex0a-x02ex0.
于是,若过点(a,b)可作曲线y=f(x)的三条切线,则方程(x02-ax0-a)ex0+b=0有三个相异的实数根.
记g(x0)=(x02-ax0-a)ex0+b,则g'(x0)=[x02+(2-a)x0-2a]ex0,
令g'(x0)=0,解得x0=-2,或x0=a∈(-2,0)
当x0∈(-∞,-2),(a,+∞)时g'(x0)>0,
当x0∈(-2,a)时g'(x0)<0,
∴当x0=-2时,g(x0)取极大值,当x0=a时,g(x0)取极小值,
如果过(a,b)可作曲线y=f(x)三条切线,即g(x0)=0有三个相异的实数根,则
即
,则
,
即-
(a+4)<b<f(a);
(2)令g'(x0)=0,解得x0=-2,或x0=a∈(-∞,-2)
当x0∈(-∞,a),(-2,+∞)时g'(x0)>0,
当x0∈(a,-2)时g'(x0)<0,
∴当x0=a时,g(x0)取极大值,当x0=-2时,g(x0)取极小值,
如果过(a,b)可作曲线y=f(x)三条切线,即g(x0)=0有三个相异的实数根,则
即f(a)<b<-
(a+4).
∴f′(x)=(x+1)ex,
∴曲线f(x)在点(x0,x0ex0)处的切线的斜率k=f′(x0)=(x0+1)ex0,
由点斜式写出切线方程为y-x0ex0=(x0+1)ex0(x-x0),即y=(x0+1)ex0x-x02ex0.
(Ⅱ)(1)如果切线过点(a,b),则存在x0,使b=(x0+1)ex0a-x02ex0.
于是,若过点(a,b)可作曲线y=f(x)的三条切线,则方程(x02-ax0-a)ex0+b=0有三个相异的实数根.
记g(x0)=(x02-ax0-a)ex0+b,则g'(x0)=[x02+(2-a)x0-2a]ex0,
令g'(x0)=0,解得x0=-2,或x0=a∈(-2,0)
当x0∈(-∞,-2),(a,+∞)时g'(x0)>0,
当x0∈(-2,a)时g'(x0)<0,
∴当x0=-2时,g(x0)取极大值,当x0=a时,g(x0)取极小值,
如果过(a,b)可作曲线y=f(x)三条切线,即g(x0)=0有三个相异的实数根,则
|
即
|
|
即-
| 1 |
| e2 |
(2)令g'(x0)=0,解得x0=-2,或x0=a∈(-∞,-2)
当x0∈(-∞,a),(-2,+∞)时g'(x0)>0,
当x0∈(a,-2)时g'(x0)<0,
∴当x0=a时,g(x0)取极大值,当x0=-2时,g(x0)取极小值,
如果过(a,b)可作曲线y=f(x)三条切线,即g(x0)=0有三个相异的实数根,则
|
即f(a)<b<-
| 1 |
| e2 |

练习册系列答案
相关题目
 和
和 (单位:千米/小时).甲、乙从起点到终点的过程中,给出下列描述:
(单位:千米/小时).甲、乙从起点到终点的过程中,给出下列描述: 与直线
与直线 围成的封闭区域为M,则区域M的面积为( )
围成的封闭区域为M,则区域M的面积为( )

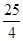

 =_______.
=_______. 则
则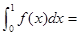 ( )
( )