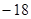题目内容
设函数f(x)=alnx-bx2(x>0),若函数f(x)在x=1处与直线y=-
相切.
(1)求实数a,b的值;
(2)求函数f(x)在[
,e]上的最大值.
| 1 |
| 2 |
(1)求实数a,b的值;
(2)求函数f(x)在[
| 1 |
| e |
(1)∵函数f(x)=alnx-bx2(x>0),∴f′(x)=
-2bx,
∵函数f(x)在x=1处与直线y=-
相切,
∴
,解得
;
(2)f(x)=lnx-
x2,f′(x)=
,
当
≤x≤e时,令f'(x)>0得
≤x<1,
令f'(x)<0,得1<x≤e,
∴f(x)在[
,1],上单调递增,
在[1,e]上单调递减,
∴f(x)max=f(1)=-
;
| a |
| x |
∵函数f(x)在x=1处与直线y=-
| 1 |
| 2 |
∴
|
|
(2)f(x)=lnx-
| 1 |
| 2 |
| 1-x2 |
| x |
当
| 1 |
| e |
| 1 |
| e |
令f'(x)<0,得1<x≤e,
∴f(x)在[
| 1 |
| e |
在[1,e]上单调递减,
∴f(x)max=f(1)=-
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
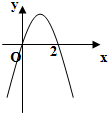
 在R上可导,
在R上可导, ,则
,则 ( )
( )