题目内容
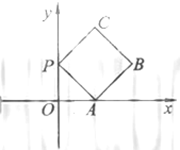
如图放置的边长为1的正方形PABC沿x轴滚动(向右为顺时针,向左为逆时针)。设顶点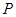 (x,y)的轨迹方程是
(x,y)的轨迹方程是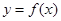 ,则关于
,则关于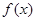 的最小正周期
的最小正周期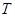 及
及 在其两个相邻零点间的图像与x轴所围区域的面积
在其两个相邻零点间的图像与x轴所围区域的面积 的正确结论是 ( )
的正确结论是 ( )
 (x,y)的轨迹方程是
(x,y)的轨迹方程是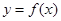 ,则关于
,则关于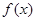 的最小正周期
的最小正周期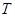 及
及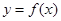 在其两个相邻零点间的图像与x轴所围区域的面积
在其两个相邻零点间的图像与x轴所围区域的面积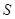 的正确结论是 ( )
的正确结论是 ( )
A. , , | B. , , |
C. , , | D. , , |
A
本题考查了图形翻转的特征,直线与圆的概念性质及圆面积的计算以及函数周期的概念。
分析:由于图形绕某一点翻转时到该改点的距离不变,所以翻转的轨迹是一个圆。这样把翻转问题转换为圆的问题。
解:由原图可以知道直线AP与直线AB斜率分别为1和-1,所以P刚开始以A为中心翻转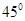 ,即B到达x轴,此时的轨迹是以A为圆心半径为
,即B到达x轴,此时的轨迹是以A为圆心半径为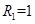 的八分之一圆;接下来是以B为圆心翻转
的八分之一圆;接下来是以B为圆心翻转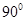 ,即C到达x轴,此时P的轨迹是以A为圆心
,即C到达x轴,此时P的轨迹是以A为圆心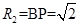 为半径的四分之一圆;同理,接下来轨迹是以C翻转
为半径的四分之一圆;同理,接下来轨迹是以C翻转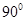 ,轨迹为以C为圆心半径
,轨迹为以C为圆心半径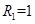 的四分之一圆,此时P恰好到达x轴;若在翻转
的四分之一圆,此时P恰好到达x轴;若在翻转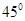 刚好回到原来的状态A在x轴上,此时P距离等于翻转后的A点到原来A的距离为4,所以周期
刚好回到原来的状态A在x轴上,此时P距离等于翻转后的A点到原来A的距离为4,所以周期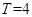 ,由翻转的角度可以知道面积为半径
,由翻转的角度可以知道面积为半径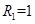 的半圆面积与
的半圆面积与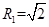 为四分之一圆的面积和,但是翻转过程成会形成两个边长为1的直角三角形,所以总面积为
为四分之一圆的面积和,但是翻转过程成会形成两个边长为1的直角三角形,所以总面积为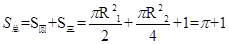 ,整个过程如图示
,整个过程如图示
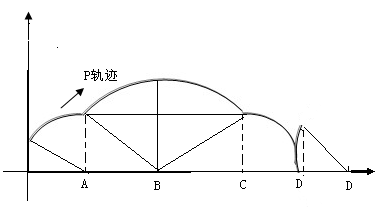
点评:本题主要考查翻转与圆的性质,数形结合画图时解决本题的关键。容易容易出错的地方在于忽略来那个三角形的面积
分析:由于图形绕某一点翻转时到该改点的距离不变,所以翻转的轨迹是一个圆。这样把翻转问题转换为圆的问题。
解:由原图可以知道直线AP与直线AB斜率分别为1和-1,所以P刚开始以A为中心翻转
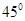 ,即B到达x轴,此时的轨迹是以A为圆心半径为
,即B到达x轴,此时的轨迹是以A为圆心半径为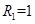 的八分之一圆;接下来是以B为圆心翻转
的八分之一圆;接下来是以B为圆心翻转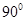 ,即C到达x轴,此时P的轨迹是以A为圆心
,即C到达x轴,此时P的轨迹是以A为圆心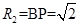 为半径的四分之一圆;同理,接下来轨迹是以C翻转
为半径的四分之一圆;同理,接下来轨迹是以C翻转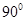 ,轨迹为以C为圆心半径
,轨迹为以C为圆心半径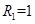 的四分之一圆,此时P恰好到达x轴;若在翻转
的四分之一圆,此时P恰好到达x轴;若在翻转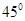 刚好回到原来的状态A在x轴上,此时P距离等于翻转后的A点到原来A的距离为4,所以周期
刚好回到原来的状态A在x轴上,此时P距离等于翻转后的A点到原来A的距离为4,所以周期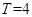 ,由翻转的角度可以知道面积为半径
,由翻转的角度可以知道面积为半径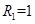 的半圆面积与
的半圆面积与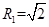 为四分之一圆的面积和,但是翻转过程成会形成两个边长为1的直角三角形,所以总面积为
为四分之一圆的面积和,但是翻转过程成会形成两个边长为1的直角三角形,所以总面积为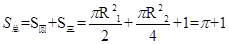 ,整个过程如图示
,整个过程如图示
点评:本题主要考查翻转与圆的性质,数形结合画图时解决本题的关键。容易容易出错的地方在于忽略来那个三角形的面积

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 的图象经过点
的图象经过点 ,则
,则 的值为 _____ .
的值为 _____ .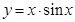 ②
②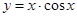 ③
③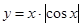 ④
④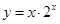 的图象(部分)如下,则按照从左到右图像对应的函数序号安排正确的一组是 ( )
的图象(部分)如下,则按照从左到右图像对应的函数序号安排正确的一组是 ( )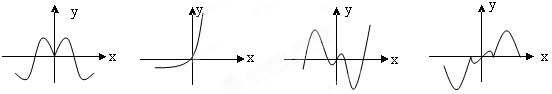
 的方程是
的方程是 ,
,  的方程是
的方程是 (
( ,
,
 表示的曲线为图中的( )
表示的曲线为图中的( )
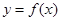 在区间
在区间 上的图象为连续不断的曲线,则下列说法正确的是( )
上的图象为连续不断的曲线,则下列说法正确的是( ) ,不存在实数
,不存在实数 使得
使得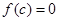 ;
; ,存在且只存在一个实数
,存在且只存在一个实数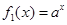 ,
,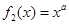 ,
,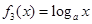 (其中
(其中 且
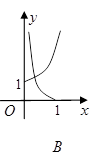
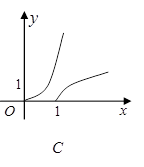
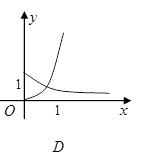
且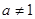 ),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图像,其中正确的是( )
),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图像,其中正确的是( )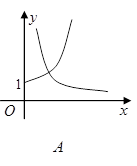
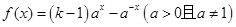 在R上既是奇函数,又是减函数,
在R上既是奇函数,又是减函数,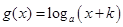 的图像是
的图像是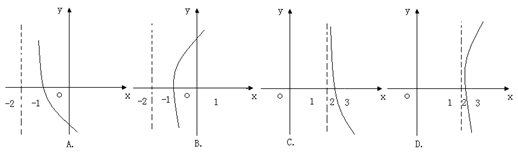
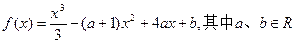
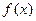 在
在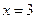 处取得极小值是
处取得极小值是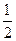 ,求
,求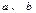 的值;
的值; 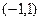 上有且只有一个极值点, 求实数
上有且只有一个极值点, 求实数 的取值范围.
的取值范围.