题目内容
 (2012•长宁区二模)棱锥的底面是正三角形,边长为1,棱锥的一条侧棱与底面垂直,其余两条侧棱与底面所成角都等于
(2012•长宁区二模)棱锥的底面是正三角形,边长为1,棱锥的一条侧棱与底面垂直,其余两条侧棱与底面所成角都等于| π | 3 |
(1)求这个棱锥的侧面积和体积;
(2)求异面直线PD与AB所成角的大小.
分析:(1)棱锥的侧面积等于三个侧面的面积的和,体积利用V=
S△ABCPA即可求解;
(2)取AC中点E,连接DE,则∠PDE为异面直线PD与AB所成角(或其补角).△PDE中,利用余弦定理可求异面直线PD与AB所成角的大小.
| 1 |
| 3 |
(2)取AC中点E,连接DE,则∠PDE为异面直线PD与AB所成角(或其补角).△PDE中,利用余弦定理可求异面直线PD与AB所成角的大小.
解答:解:(1)∵PA⊥平面ABC,两条侧棱与底面所成角都等于
,∴∠PBA=∠PCA=
,
∵AB=AC=1,∴PA=
,PB=PC=2,….(2分)
∵D为BC中点,∴PD⊥BC,∴PD=
=
,….(3分)
∴S侧=2×
×1×
+
×1×
=
,….(5分)
V=
S△ABCPA=
….(6分)
(2)取AC中点E,连接DE,
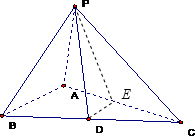
则DE∥AB,∴∠PDE为异面直线PD与AB所成角(或其补角).….(8分)
△PDE中,DE=
,PE=
,….(10分)
设∠PDE=θ,则cosθ=
=
,….(12分)
因此异面直线PD与AB所成角的大小为arccos
.….(14分)
| π |
| 3 |
| π |
| 3 |
∵AB=AC=1,∴PA=
| 3 |
∵D为BC中点,∴PD⊥BC,∴PD=
| PB2-BD2 |
| ||
| 2 |
∴S侧=2×
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
4
| ||||
| 4 |
V=
| 1 |
| 3 |
| 1 |
| 4 |
(2)取AC中点E,连接DE,

则DE∥AB,∴∠PDE为异面直线PD与AB所成角(或其补角).….(8分)
△PDE中,DE=
| 1 |
| 2 |
| ||
| 2 |
设∠PDE=θ,则cosθ=
| PD2+DE2-PE2 |
| 2PD•DE |
| ||
| 10 |
因此异面直线PD与AB所成角的大小为arccos
| ||
| 10 |
点评:本题考查棱锥的侧面积和体积,考查异面直线所成的角,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目