题目内容
15. 如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;
如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;(1)当$θ=\frac{π}{12}$时,求四边形ABCD的面积.
(2)若要在景区内铺设一条由线段AB,BC,CD和DA组成的观光道路,则当θ为何值时,观光道路的总长l最长,并求出l的最大值.
分析 (1)连接OD,则∠COD=$\frac{π}{12}$,∠AOD=$\frac{5}{6}$π,即可求出四边形ABCD的面积;
(2)利用余弦定理求出BC,CD,DA,可得l,利用换元、配方法,即可得出结论
解答 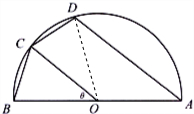 解:(1)连接OD,则∠COD=$\frac{π}{12}$,∠AOD=$\frac{5}{6}$π,∴四边形ABCD的面积为2×$\frac{1}{2}$×1×1×sin$\frac{π}{12}$+$\frac{1}{2}$×1×1×sin$\frac{5}{6}$π=$\frac{\sqrt{6}-\sqrt{2}}{4}$+$\frac{1}{4}$;
解:(1)连接OD,则∠COD=$\frac{π}{12}$,∠AOD=$\frac{5}{6}$π,∴四边形ABCD的面积为2×$\frac{1}{2}$×1×1×sin$\frac{π}{12}$+$\frac{1}{2}$×1×1×sin$\frac{5}{6}$π=$\frac{\sqrt{6}-\sqrt{2}}{4}$+$\frac{1}{4}$;
(2)由题意,BC=CD=$\sqrt{2-2cosθ}$=2sin$\frac{θ}{2}$,DA=$\sqrt{2+2cos2θ}$=2cosθ,
∴l=2+4sin$\frac{θ}{2}$+2cosθ(0<θ<$\frac{π}{2}$),
令t=sin$\frac{θ}{2}$,则(0<t<$\frac{\sqrt{2}}{2}$),l=-4(t-$\frac{1}{2}$)2+5,
∴t=$\frac{1}{2}$时,即θ=$\frac{π}{3}$,l的最大值为5.
点评 本题考查余弦定理,考查学生的计算能力,确定函数的解析式是关键.

练习册系列答案
相关题目
6.函数y=cos2x-sin2x的图象可以由函数y=cos2x+sin2x的图象经过下列哪种变换得到( )
| A. | 向右平移$\frac{3π}{4}$ | B. | 向右平移π | C. | 向左平移$\frac{π}{2}$ | D. | 向左平移π |
7.下列说法正确的是( )
| A. | 若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行 | |
| B. | 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 | |
| C. | 垂直于同一直线的两条直线相互平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行 |