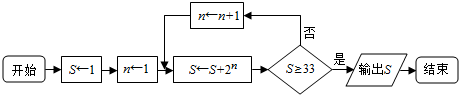
题目内容
5.已知函数f(x)=alnx-x,a∈R.(1)求函数f(x)的单调区间;
(2)若函数f(x)有两个不同的零点x1、x2,且x1<x2.
①求实数a的取值范围;
②试比较x1+x2与2e(e为自然对数的底数)的大小,并证明你的结论.
分析 (1)先求导,再分类讨论,根据导数和函数单调性的关系即可求出.
(2)①通过求导,得出切点坐标,找到函数y=f(x)有两个零点的等价条件,从而求出a的取值范围;
②x1=alnx1,x2=alnx2,令$\frac{{x}_{2}}{{x}_{1}}$=t,t>1,用含t的式子表示x1,x2,得到x1+x2=$\frac{a(t+1)lnt}{t-1}$,构造函数,求出函数的最小值为2a,问题得以解决.
解答 解:(1)f′(x)=$\frac{a}{x}$-1=$\frac{a-x}{x}$,x>0
当a≤0时,f′(x)<0恒成立,
∴函数f(x)在(0,+∞)上单调递减,
当a>0时,
令f′(x)=0,解得x=a,
当f′(x)>0,即0<x<a时,函数单调递增,
当f′(x)<0,即x>a时,函数单调递减,
综上所述:当a≤0时,函数f(x)在(0,+∞)上单调递减,
当a>0时,函数f(x)在(a,+∞)上单调递减,在(0,a)上单调递增;
(2)令f(x)=0,∴lnx=$\frac{1}{a}$x,
画出函数g(x)=lnx,h(x)=$\frac{1}{a}$x的图象,如图示: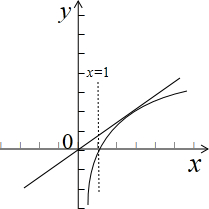 ,
,
∵g′(x)=$\frac{1}{x}$=$\frac{1}{a}$,∴切点坐标是(a,lna),
把(a,lna)代入h(x)=$\frac{1}{a}$x,得:a=e,
∴若y=f(x)有两个零点x1,x2,
即g(x),h(x)有2个交点,只需a>e即可;
∴a的范围是(e,+∞):
②∵x1=alnx1,x2=alnx2,
∴x2-x1=aln$\frac{{x}_{2}}{{x}_{1}}$,
令$\frac{{x}_{2}}{{x}_{1}}$=t,t>1
则$\left\{\begin{array}{l}{{x}_{2}-{x}_{1}=alnt}\\{{x}_{2}=t{x}_{1}}\end{array}\right.$,
解得x1=$\frac{alnt}{t-1}$,x2=$\frac{atlnt}{t-1}$,
∴x1+x2=$\frac{alnt}{t-1}$+=$\frac{atlnt}{t-1}$=$\frac{a(t+1)lnt}{t-1}$
令m(x)=$\frac{a(x+1)lnx}{x-1}$,(x>1),
则m′(x)=$\frac{a({x}^{2}-1-2xlnx)}{x(x-1)^{2}}$,
∵a>e,x(x-1)2>0,
令n(x)=x2-2xlnx-1,
则n′(x)=2(x-lnx-1)>0,
∴n(x)在(1,+∞)递增,
∴n(x)>n(1)=0,
∴m′(x)>0,m(x)在(1,+∞)递增,
根据洛必达法则,$\underset{lim}{x→1}$$\frac{a(x+1)lnx}{x-1}$=$\underset{lim}{x→1}$$\frac{a(1+\frac{x+1}{x})}{1}$=2a,
∵a>e,
∴2a>2e,
∴x1+x2>2e
点评 本题考查了导数的运算以及利用导数研究函数的单调性与极值问题,也考查了函数思想、化归思想、抽象概括能力和分析问题、解决问题的能力,是综合型题目,属于难题.

| x | $\frac{2π}{3}$ | x1 | $\frac{8π}{3}$ | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,若直线y=k与函数y=f(x)g(x)的图象在[0,π]上有交点,求实数k的取值范围.
| A. | $\frac{54}{125}$ | B. | $\frac{36}{125}$ | C. | $\frac{27}{125}$ | D. | $\frac{18}{25}$ |
 如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;
如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;