题目内容
若一个圆锥的轴截面是边长为2的正三角形,则这个圆锥的体积为( )A.
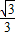 π
πB.
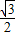 π
πC.
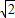 π
πD.2π
【答案】分析:根据圆角轴截面的定义结合正三角形的性质,可得圆锥底面半径长和高的大小,由此结合圆锥的体积公式,则不难得到本题的答案.
解答:解: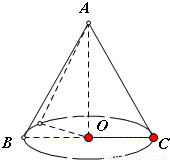 ∵圆锥的轴截面是正三角形ABC,边长等于2
∵圆锥的轴截面是正三角形ABC,边长等于2
∴圆锥的高AO=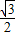 ×2=
×2=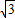 ,
,
底面半径r= ×2=1
×2=1
因此,该圆锥的体积V= πr2•AO=
πr2•AO= π×12×
π×12×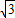 =
=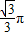
故选A
点评:本题给出圆锥轴截面的形状,求圆锥的体积,着重考查了等边三角形的性质和圆锥的轴截面等知识,属于基础题.
解答:解:
 ∵圆锥的轴截面是正三角形ABC,边长等于2
∵圆锥的轴截面是正三角形ABC,边长等于2∴圆锥的高AO=
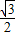 ×2=
×2=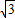 ,
,底面半径r=
 ×2=1
×2=1因此,该圆锥的体积V=
 πr2•AO=
πr2•AO= π×12×
π×12×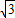 =
=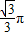
故选A
点评:本题给出圆锥轴截面的形状,求圆锥的体积,着重考查了等边三角形的性质和圆锥的轴截面等知识,属于基础题.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
若一个圆锥的轴截面是等边三角形,其面积为
,则这个圆锥的全面积是( )
| 3 |
| A、3π | ||
B、3
| ||
| C、6π | ||
| D、9π |