题目内容
平面直角坐标系xoy中,动点 满足:点P到定点
满足:点P到定点 与到y轴的距离之差为
与到y轴的距离之差为 .记动点P的轨迹为曲线C.
.记动点P的轨迹为曲线C.
(1)求曲线C的轨迹方程;
(2)过点F的直线交曲线C于A、B两点,过点A和原点O的直线交直线 于点D,求证:直线DB平行于x轴.
于点D,求证:直线DB平行于x轴.
(1)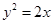 ,(2)详见解析.
,(2)详见解析.
解析试题分析:(1)求动点轨迹方程,首先设动点坐标,本题已设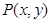 ,其次列动点满足条件
,其次列动点满足条件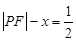 ,然后利用坐标化简关系式,即
,然后利用坐标化简关系式,即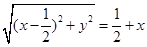 ,
,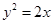 ,最后要考虑动点满足限制条件,本题为已知条件
,最后要考虑动点满足限制条件,本题为已知条件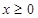 ,另外本题对条件
,另外本题对条件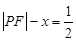 的化简也可从抛物线的定义上理解,这样更快,(2)证明直线平行于
的化简也可从抛物线的定义上理解,这样更快,(2)证明直线平行于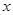 轴,可利用斜率为零,或证明纵坐标相等,总之都需要从坐标出发.注意到点在抛物线上,设点的坐标可简洁,设
轴,可利用斜率为零,或证明纵坐标相等,总之都需要从坐标出发.注意到点在抛物线上,设点的坐标可简洁,设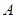 的坐标为
的坐标为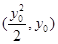 ,利用
,利用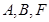 三点共线解出点
三点共线解出点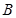 的纵坐标为
的纵坐标为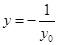 ,根据直线
,根据直线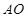 与直线
与直线 的交点解出
的交点解出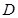 的纵坐标也为
的纵坐标也为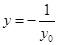 .
.
试题解析:(1)依题意: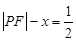 2分
2分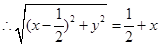
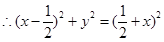 4分
4分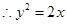 6分
6分
注:或直接用定义求解.
(2)法1:设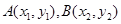 ,直线
,直线 的方程为
的方程为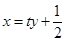
由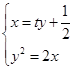 得
得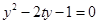 8分
8分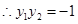
直线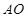 的方程为
的方程为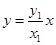
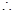 点
点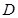 的坐标为
的坐标为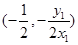 2分
2分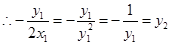
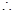 直线
直线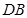 平行于
平行于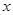 轴. 14分
轴. 14分
法2:设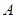 的坐标为
的坐标为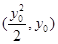 ,则
,则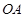 的方程为
的方程为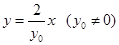
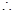 点
点 的纵坐标为
的纵坐标为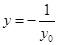 , 8分
, 8分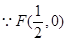
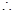 直线
直线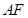 的方程为
的方程为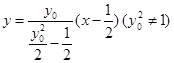
 点
点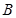 的纵坐标为
的纵坐标为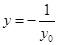 . 12分
. 12分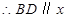 轴;当
轴;当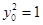 时,结论也成立,
时,结论也成立, 直线
直线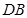 平行于
平行于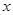 轴. 14分
轴. 14分
考点:轨迹方程,直线与抛物线位置关系

练习册系列答案
相关题目
 和
和 ,且|
,且|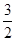 )在该椭圆上.
)在该椭圆上. 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A ,求以
,求以 =
=
 .
. .若存在,请求出点B的坐标;若不存在,请说明理由.
.若存在,请求出点B的坐标;若不存在,请说明理由. :
: 的离心率为
的离心率为 ,右焦点
,右焦点 到直线
到直线 的距离为
的距离为 .
. 的方程;
的方程; (
( )的直线
)的直线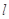 与椭圆
与椭圆 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线 于点
于点 ,线段
,线段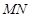 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值. 的三个顶点都在抛物线
的三个顶点都在抛物线 上,且抛物线的焦点
上,且抛物线的焦点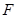 满足
满足 ,若
,若 边上的中线所在直线
边上的中线所在直线 的方程为
的方程为 (
( 为常数且
为常数且 ).
). 的值;
的值; 为抛物线的顶点,
为抛物线的顶点, ,
, ,
, 的面积分别记为
的面积分别记为 ,
, ,
,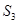 ,求证:
,求证: 为定值.
为定值. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
. +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当|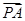 -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围. 的直线
的直线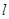 交椭圆
交椭圆 于
于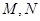 两点,
两点, 是椭圆的一个顶点,若线段
是椭圆的一个顶点,若线段 的中点恰为点
的中点恰为点 .
. 的面积.
的面积.