题目内容
已知 的三个顶点都在抛物线
的三个顶点都在抛物线 上,且抛物线的焦点
上,且抛物线的焦点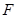 满足
满足 ,若
,若 边上的中线所在直线
边上的中线所在直线 的方程为
的方程为 (
( 为常数且
为常数且 ).
).
(1)求 的值;
的值;
(2) 为抛物线的顶点,
为抛物线的顶点, ,
, ,
, 的面积分别记为
的面积分别记为 ,
, ,
,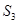 ,求证:
,求证: 为定值.
为定值.
(1)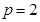 ;(2)详见试题解析.
;(2)详见试题解析.
解析试题分析:(1)由已知,抛物线的焦点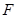 满足
满足 ,从而知BC边上的中点
,从而知BC边上的中点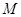 符合
符合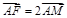 ,因此点
,因此点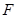 在直线
在直线 上,令
上,令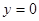 ,可得抛物线的焦点
,可得抛物线的焦点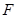 的坐标,由此可求得
的坐标,由此可求得 的值;(2)首先设出
的值;(2)首先设出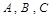 的坐标:
的坐标: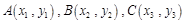 ,由已知
,由已知 ,即可得
,即可得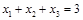 ,而
,而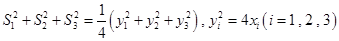 ,最终即可证得
,最终即可证得 为定值.
为定值.
试题解析:(1)因为抛物线的焦点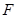 满足
满足 ,取BC边上的中点
,取BC边上的中点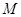 ,则
,则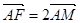 ,故点
,故点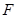 在直线
在直线 上,令
上,令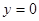 ,得
,得 ,得抛物线的焦点
,得抛物线的焦点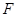
 ,于是,
,于是,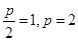 . 5分
. 5分
(2)记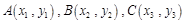 ,由
,由 知:
知: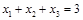 , 7分
, 7分
且 .于是,
.于是,
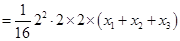
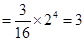 .证毕. 13分
.证毕. 13分
考点:1.抛物线的标准方程及其简单几何性质;2.直线与抛物线的位置关系;3.解析几何中定值问题的解法.

练习册系列答案
相关题目
 -
- =1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.
=1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.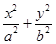 =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.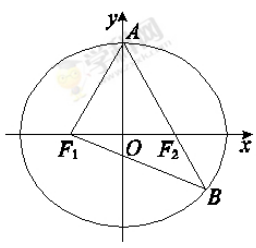
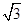 ,求a,b的值.
,求a,b的值. 满足:点P到定点
满足:点P到定点 与到y轴的距离之差为
与到y轴的距离之差为 .记动点P的轨迹为曲线C.
.记动点P的轨迹为曲线C. 于点D,求证:直线DB平行于x轴.
于点D,求证:直线DB平行于x轴.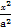 +
+ =1(a>b>0).
=1(a>b>0). ,求椭圆的标准方程.
,求椭圆的标准方程. .
. 的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设
的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设 =t
=t ,求实数t的值.
,求实数t的值.
 的抛物线
的抛物线 的焦点
的焦点 与椭圆
与椭圆 的右焦点重合,
的右焦点重合, 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为 .
. 的正三角形,求抛物线
的正三角形,求抛物线 ,求椭圆
,求椭圆 ;
; 为椭圆
为椭圆 、
、 分别与
分别与 轴交于点
轴交于点 和
和 ,证明:
,证明: .
. =1(a>b>0)的左焦点为F,短轴端点为B1、B2,
=1(a>b>0)的左焦点为F,短轴端点为B1、B2, =2b2.
=2b2.