题目内容
在xOy平面上有一系列点P1（x1,y1）,P2(x2,y2),…，Pn(xn,yn),…,对每个自然数n,点Pn位于函数y=x2(x≥0)的图象上，以点Pn为圆心的⊙Pn与x轴都相切，且⊙Pn与⊙Pn+1又彼此外切.若x1=1且xn+1＜xn?(n∈N*).(1)求证：数列{1xn}是等差数列；
(2)设⊙Pn的面积为Sn,Tn=
+…+
,求证：Tn＜
.
(1)证明：依题意，⊙Pn的半径rn=yn=xn2,∵⊙Pn与⊙Pn+1彼此外切，∴|PnPn+1|=rn+rn+1|,∴=yn+yn+1，两边平方，化简得（xn-xn+1）2=4ynyn+1,即：（xn-xn+1）2=4xn2xn+12.∵0＜xn+1＜xn,∴xn-xn+1=2xnxn+1=2(n∈N*).所以数列{
}是等差数列；
(2)解析：由题设，∵x1=1,∴
=
+(n-1)·2
xn=
,
∴Sn=πrn2=πyn2=πxn4=
,
Tn=
+…+
=
［1+
+…+
］
≤
［1+
+…+
］=
［1+
(1-
)］=
＜
.
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
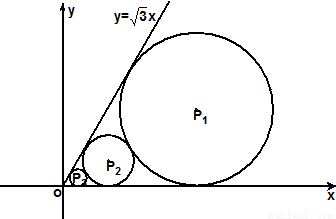
在xoy平面上有一系列点P1（x1，y1），P2（x2，y2）…，Pn（xn，yn），…，（n∈N*），点Pn在函数y=x2（x≥0）的图象上，以点Pn为圆心的圆Pn与x轴都相切，且圆Pn与圆Pn+1又彼此外切．若x1=1，且xn+1＜xnx1=1．
在xoy平面上有一系列点P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），…，对每个正整数n，以点Pn为圆心的⊙Pn与x轴及射线y=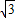
x，（x≥0）都相切，且⊙Pn与⊙Pn+1彼此外切．若x1=1，且xn+1＜xn（n∈N*）．
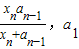=1，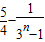
，（n≥2）
．