题目内容
 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2)…,Pn(xn,yn),…,(n∈N*),点Pn在函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xnx1=1.
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2)…,Pn(xn,yn),…,(n∈N*),点Pn在函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xnx1=1.(I)求数列{xn}的通项公式;
(II)设圆Pn的面积为Sn,Tn=
| S1 |
| S2 |
| Sn |
3
| ||
| 2 |
分析:(I)由题意圆Pn与Pn+1彼此外切,利用两圆外切等价于两圆心距等于圆的半径,化简出数列{xn}的递推关系,进而得到数列{xn}的通项公式.
(II)由于圆Pn的面积为Sn利用圆的面积公式求出,又有题中Tn的式子特点,利用裂项相消法,求出Tn,在利用简单的去一项即可得证.
(II)由于圆Pn的面积为Sn利用圆的面积公式求出,又有题中Tn的式子特点,利用裂项相消法,求出Tn,在利用简单的去一项即可得证.
解答:解:(I)圆Pn与Pn+1彼此外切,令rn为圆Pn的半径,
∴|PnPn+1|=rn+rn+1即
=yn+yn+1
两边平方并化简得(xn-xn+1)2=4ynyn+1
由题意得,圆Pn的半径rn=yn=xn2,(xn-xn+1)2=4xn2xn+12
∵xn>xn+1>0;∴xn-xn+1=2xnxn+1,即
-
=2(n∈N+)
∴数列{
}是以
=1为首项,以2为公差的等差数列,
所以
=1+(n-1)×2=2n-1,即xn=
(II)Sn=π
=π
=π
=
,
因为Tn=
+
+…+
=
[1+
+…+
]
≤
(1+
+
+…+
)
=
{1+
[(1-
)+(
-
)+…+(
-
)]}=
[1+
(1-
)]=
-
<
所以,Tn<
∴|PnPn+1|=rn+rn+1即
| (xn-xn+1)2+(yn-yn+1)2 |
两边平方并化简得(xn-xn+1)2=4ynyn+1
由题意得,圆Pn的半径rn=yn=xn2,(xn-xn+1)2=4xn2xn+12
∵xn>xn+1>0;∴xn-xn+1=2xnxn+1,即
| 1 |
| xn+1 |
| 1 |
| xn |
∴数列{
| 1 |
| xn |
| 1 |
| x1 |
所以
| 1 |
| xn |
| 1 |
| 2n-1 |
(II)Sn=π
| r | n 2 |
| y | n 2 |
| x | n 4 |
| π |
| (2n-1)4 |
因为Tn=
| S1 |
| S2 |
| Sn |
| x |
| 1 |
| 32 |
| 1 |
| (2n-1)2 |
≤
| π |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2n-3)(2n-1) |
=
| π |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-3 |
| 1 |
| 2n-1 |
| π |
| 1 |
| 2 |
| 1 |
| 2n-1 |
3
| ||
| 2 |
| ||
| 2(2n-1) |
3
| ||
| 2 |
所以,Tn<
3
| ||
| 2 |
点评:此题重点考查了两元相外切的等价条件,还考查了有数列的递推关系求其通项公式,及裂项相消的求和方法,还考查了去一项进行了简单的放缩.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
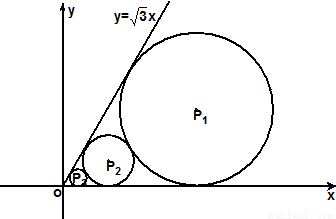
 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=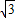 x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).
x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).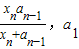 =1,
=1,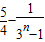 ,(n≥2)
,(n≥2)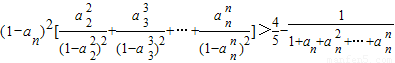 .
.