题目内容
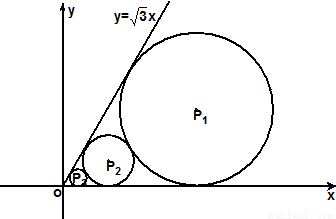
 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=| 3 |
(1)求证:数列{xn}是等比数列,并求数列{xn}的通项公式;
(2)设数列{an}的各项为正,且满足an≤
| xnan-1 |
| xn+an-1 |
求证:a1x1+a2x2+a3x3+…+anxn<
| 5 |
| 4 |
| 1 |
| 3n-1 |
(3)对于(2)中的数列{an},当n>1时,求证:(1-an)2[
| ||
(1-
|
| ||
(1-
|
| ||
(1-
|
| 4 |
| 5 |
| 1 | ||||
1+an+
|
分析:(1)由圆Pn与P(n+1)相切,且P(n+1)与x轴相切可知Rn=Yn,R(n+1)=Y(n+1),且两圆心间的距离就等于两半径之和进而得到
=
=
(xn+xn+1),整理得证.
(2)由an≤
,可证an≤
,进而得Sn=a1x1+a2x2+a3x3+…+anxn≤1×1+
×
+
×
+…+
×
从而可证
(3)先证a1>a2>…>an>0,再令:bk=
,从而bk=
≥
=
利于放缩法可证.
| (xn-xn+1)2+(yn-yn+1)2 |
|
| ||
| 3 |
(2)由an≤
| xnan-1 |
| xn+an-1 |
| 2 |
| 3n-1 |
| 2 |
| 8 |
| 1 |
| 3 |
| 2 |
| 26 |
| 1 |
| 9 |
| 2 |
| 3n-1 |
| 1 |
| 3n-1 |
(3)先证a1>a2>…>an>0,再令:bk=
(1-an)2
| ||
(1-
|
(1-an)2
| ||
(1-
|
(1-ak)2
| ||
(1-
|
| ||||
(1+ak+
|
解答:解:(1)点列P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…必在射线y=
x,(x≥0),
∴yn=
为⊙Pn的半径,
∵⊙Pn与⊙Pn+1外切,
∴
=
=
(xn+xn+1)①…(3分)
化简①式得:3xn+12-10xnxn+1+3xn2=0,解得:xn+1=3xn或xn+1=
xn,
∵xn+1<xn,∴xn+1=
xn,∴数列{xn}是等比数列,∵x1=1,则xn=(
)n-1…(5分)
(2)an≤
,而an>0,xn>0,
∴
≥
+
⇒
-
≥
,∴
-
≥
+
+…+
,∵a1=1,
∴
≥1+
+
+…+
=1+3+32+…+3n-1=
∴an≤
…(8分)
设Sn=a1x1+a2x2+a3x3+…+anxn,Tn=
-
∵Sn=a1x1+a2x2+a3x3+…+anxn≤1×1+
×
+
×
+…+
×
当n=2时,S2≤1+
=
,T2=
-
=
,必有S2<T2
当n>2时,
∵anxn≤
<
<
=
-
∴Sn<1+
+(
-
)+(
-
)+…+(
-
)=1+
+
-
=
-
<
-
…(13分)
(3)∵
-
≥
>0∴an<an-1,∴1=a1>a2>…>an>0
令:bk=
,则bk=
≥
=
>
=
-
>
-
=
-
…(18分)
∵0<a2<
=
∴(1-an)2[
+
+…+
]=
bk>
(
-
)=
-
>
-
…20分.
| ||
| 3 |
∴yn=
| xn | ||
|
∵⊙Pn与⊙Pn+1外切,
∴
| (xn-xn+1)2+(yn-yn+1)2 |
|
| ||
| 3 |
化简①式得:3xn+12-10xnxn+1+3xn2=0,解得:xn+1=3xn或xn+1=
| 1 |
| 3 |
∵xn+1<xn,∴xn+1=
| 1 |
| 3 |
| 1 |
| 3 |
(2)an≤
| xnan-1 |
| xn+an-1 |
∴
| 1 |
| an |
| 1 |
| xn |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| xn |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| x2 |
| 1 |
| x3 |
| 1 |
| xn |
∴
| 1 |
| an |
| 1 |
| x2 |
| 1 |
| x3 |
| 1 |
| xn |
| 3n-1 |
| 2 |
∴an≤
| 2 |
| 3n-1 |
设Sn=a1x1+a2x2+a3x3+…+anxn,Tn=
| 5 |
| 4 |
| 1 |
| 3n-1 |
∵Sn=a1x1+a2x2+a3x3+…+anxn≤1×1+
| 2 |
| 8 |
| 1 |
| 3 |
| 2 |
| 26 |
| 1 |
| 9 |
| 2 |
| 3n-1 |
| 1 |
| 3n-1 |
当n=2时,S2≤1+
| 1 |
| 12 |
| 13 |
| 12 |
| 5 |
| 4 |
| 1 |
| 32-1 |
| 9 |
| 8 |
当n>2时,
∵anxn≤
| 2 |
| (3n-1)3n-1 |
| 2 |
| (3n-1)(3n-1-1) |
| 2•3n-1 |
| (3n-1)(3n-1-1) |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
∴Sn<1+
| 1 |
| 12 |
| 1 |
| 32-1 |
| 1 |
| 33-1 |
| 1 |
| 33-1 |
| 1 |
| 34-1 |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
| 1 |
| 12 |
| 1 |
| 8 |
| 1 |
| 3n-1 |
| 29 |
| 24 |
| 1 |
| 3n-1 |
| 5 |
| 4 |
| 1 |
| 3n-1 |
(3)∵
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| xn |
令:bk=
(1-an)2
| ||
(1-
|
(1-an)2
| ||
(1-
|
(1-ak)2
| ||
(1-
|
| ||||
(1+ak+
|
| ||||||||||
(1+ak+
|
| 1 | ||||
1+ak+
|
| 1 | ||||||
1+ak+
|
| 1 | ||||
1+ak+
|
| 1 | ||||||
1+ak+1+
|
| 1 | |||||
|
| 1 | |||||
|
∵0<a2<
| 2 |
| 32-1 |
| 1 |
| 4 |
| ||
(1-
|
| ||
(1-
|
| ||
(1-
|
| n |
 |
| k=2 |
| n |
 |
| k=2 |
| 1 | |||||
|
| 1 | |||||
|
| 1 |
| 1+a2 |
| 1 | ||||
1+an+
|
| 4 |
| 5 |
| 1 | ||||
1+an+
|
点评:本题以相切为素材,考查数列与解析几何的综合,考查数列与不等式,技巧性强,难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2)…,Pn(xn,yn),…,(n∈N*),点Pn在函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xnx1=1.
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2)…,Pn(xn,yn),…,(n∈N*),点Pn在函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xnx1=1.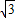 x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).
x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).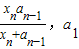 =1,
=1,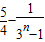 ,(n≥2)
,(n≥2)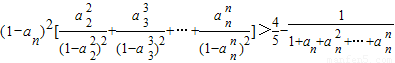 .
.