Question

【题目】如图，已知矩形ABCD中，AB＝2，AD＝1．将矩形沿对角线BD折起，使A移到点P，P在平面BCD上的投影O恰好落在CD边上．

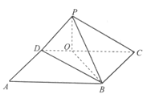
（1）证明：DP⊥平面BCP；

（2）求点O到平面PBD的距离．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）由已知可证BC⊥CD，DA⊥AB，由A点移动到了P点，可证PD⊥PB，过P点作PO⊥CD，利用PO⊥面BCD，可证BC⊥面PCD，利用线面垂直的性质得BC⊥PD，根据线面垂直的判定定理可证PD⊥面PBC．

（2）连接OB，由（1）可知DP⊥PC，可求PC，可证OP⊥CD，由DCPO＝DPPC，解得OP，OC的值，可得S△ODB，设点O到平面PBD的距离为h，可得S△DPB＝S△ABD＝1，根据VP﹣DOB＝VO﹣DPB，即可解得h的值．

（1）∵四边形ABCD为矩形，

∴BC⊥CD，DA⊥AB，

∵A点移动到了P点，

∴PD⊥PB，

又∵P点在平面BCD上的射影在CD上，

∴过P点作PO⊥CD，

∴PO⊥面BCD，

∴BC⊥面PCD，可得：BC⊥PD，

∴PD⊥面PBC，

（2）连接OB，由（1）可知DP⊥平面BCP，PC平面BCP，

所以DP⊥PC，

即PC，

由（1）可知OP⊥平面BCD，

而CD平面BCD，

所以OP⊥CD，

由DCPO＝DPPC，解得：OP，

所以OC，

可得：OD，BD，sin∠ODB，

可得S△ODBsin∠ODB，

设点O到平面PBD的距离为h，可得S△DPB＝S△ABD＝1，

因为VP﹣DOB＝VO﹣DPB，

所以S△DOBPOS△DPBh，

可得：h，解得h．

即点O到平面PBD．