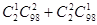题目内容
某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原节目单中,那么不同插法的种数为( )
| A.42 | B.30 | C.20 | D.12 |
A
解析试题分析:原定的5个节目之间有6个位。当插入的这两个新节目在一起时,有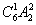 插法;当插入的这两个新节目不在一起时,有
插法;当插入的这两个新节目不在一起时,有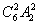 插法,所以总的不同插法的种数为
插法,所以总的不同插法的种数为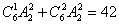 种。故选A。
种。故选A。
考点:排列和组合
点评:关于排列和组合的题目,常用到捆绑法和插位法。捆绑法是将一些对象看作一个对象进行排列;插位法是将一些对象进行排列后,再对剩下的对象进行排列。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
在 的二项展开式中,
的二项展开式中, 的系数为 ( )
的系数为 ( )
| A.-120 | B.120 | C.-15 | D.15 |
设 ,则二项式
,则二项式 展开式中的
展开式中的 项的系数为( )
项的系数为( )
A. | B.20 |
C. | D.160 |
 展开式的第6项系数最大,则其常数项为( )
展开式的第6项系数最大,则其常数项为( )
| A.120 | B.252 | C.210 | D.45 |
三角形的三边均为整数,且最长的边为11,则这样的三角形的个数有( )个。
| A.25 | B.26 | C.32 | D.36 |
现需编制一个八位的序号,规定如下:序号由4个数字和2个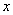 、1个
、1个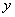 、1个
、1个 组成;2个
组成;2个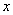 不能连续出现,且
不能连续出现,且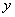 在
在 的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )
的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )
| A.12600 | B.6300 | C.5040 | D.2520 |
由数字1,2,3,4,5组成没有重复数字的五位数,其中偶数共有 ( )
| A.60个 | B.48个 | C.36个 | D.24个 |
 的展开式中,只有第5项的二项式系数最大,则展开式中的第6项是 ()
的展开式中,只有第5项的二项式系数最大,则展开式中的第6项是 ()