题目内容

椭圆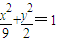的焦点为F1、F2，点P在椭圆上，若|PF1|=4，则=    ．
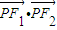【答案】分析：由|PF1|+|PF2|=6，且|PF1|=4，易得|PF2|；再根据三角形三边已求得，用余弦定理求解cos∠F1PF2；代入即可得到结论．．
解答：解：∵|PF1|+|PF2|=2a=6，
∴|PF2|=6-|PF1|=2．
在△F1PF2中，
∵cos∠F1PF2===-．
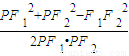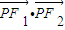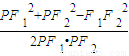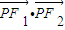∴=||•||•cos∠F1PF2=-4．
故答案为：-4．
点评：本题主要考查椭圆定义的应用及焦点三角形问题，这类题是常考类型，难度不大，考查灵活，特别是对曲线的定义和性质考查的很到位．
练习册系列答案
相关题目
（2011•韶关模拟）椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的一个焦点F与抛物线y2=4x的焦点重合，且截抛物线的准线所得弦长为
2
，倾斜角为45°的直线l过点F．
（Ⅰ）求该椭圆的方程；
（Ⅱ）设椭圆的另一个焦点为F1，问抛物线y2=4x上是否存在一点M，使得M与F1关于直线l对称，若存在，求出点M的坐标，若不存在，说明理由．
椭圆的焦点为F1，
F
 
2
，过点F1作直线与椭圆相交，被椭圆截得的最短的弦长MN长为
32
5
，△MF2N的周长为20，则椭圆的离心率为（　　）
（2012•甘肃一模）设椭圆M：
x2
a2
+
y2
2
=1(a＞
2
)的右焦点为F1，直线l：x=
a2
a2-2
与x轴交于点A，若
OF1
+2
AF1
=0（其中O为坐标原点）．
（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求
PE
•
PF
的最大值．
（2014•江门模拟）已知抛物线Σ1：y=
1
4
x2的焦点F在椭圆Σ2：
x2
a2
+
y2
b2
=1（a＞b＞0）上，直线l与抛物线Σ1相切于点P（2，1），并经过椭圆Σ2的焦点F2．
（1）求椭圆Σ2的方程；
（2）设椭圆Σ2的另一个焦点为F1，试判断直线FF1与l的位置关系．若相交，求出交点坐标；若平行，求两直线之间的距离．
如图,已知椭圆的焦点为F1、F2,A、B为顶点,离心率e=.

(1)求证:A、F1、B、F2四点共圆;

(2)以BF1为直径,作半圆O1,AF切半圆于E,交F1B延长线于F,求cosF的值.

图20

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网