题目内容
如图,已知椭圆的焦点为F1、F2,A、B为顶点,离心率e=(1)求证:A、F1、B、F2四点共圆;
(2)以BF1为直径,作半圆O1,AF切半圆于E,交F1B延长线于F,求cosF的值.

图20
解析:(1)∵![]() =
=![]() ,∴a2=
,∴a2=
又a2=b2+c2,∴b2+c2=
∴b=c,即OA=OF1=OB=OF2.
∴四边形AF1BF2是正方形.∴A、F1、B、F2四点共圆.
(2)连结O1E.∵AF切⊙O1于E,∴O1E⊥AF.
∴△O1EF∽△AF![]() .
.
∴F
∴BF=![]() EF.∴O1B=
EF.∴O1B=![]() EF,BO1=O1B+BF=
EF,BO1=O1B+BF=![]() EF.∴cosF=
EF.∴cosF=![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
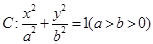 的焦点为
的焦点为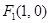 、
、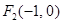 ,离心率为
,离心率为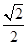 ,过点
,过点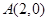 的直线
的直线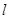 交椭圆
交椭圆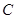 于
于 、
、 两点.
两点.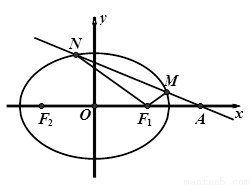
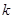 的取值范围;
的取值范围;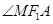 和
和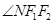 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由.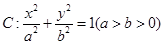 的焦点和上顶点分别为
的焦点和上顶点分别为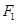 、
、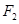 、
、 ,我们称
,我们称 为椭圆
为椭圆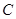 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.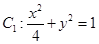 和
和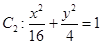 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出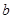 的椭圆为
的椭圆为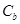 ,且直线
,且直线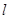 与椭圆为
与椭圆为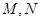 (异于端点),试问:当
(异于端点),试问:当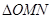 面积最大时,
面积最大时,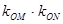 是否与
是否与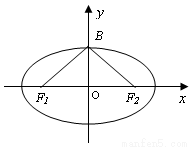
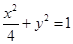 的焦点为
的焦点为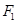 、
、 ,点
,点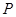 为椭圆上任意一点,过
为椭圆上任意一点,过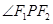 的外角平分线的垂线,垂足为点
的外角平分线的垂线,垂足为点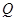 ,过点
,过点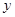 轴的垂线,垂足为
轴的垂线,垂足为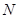 ,线段
,线段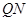 的中点为
的中点为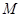 ,则点
,则点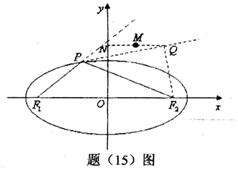
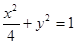 的焦点为F1,F2,点P为椭圆上任意一点,过F2作
的焦点为F1,F2,点P为椭圆上任意一点,过F2作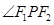 的外角平分线的垂线,垂足为点Q,过点Q作
的外角平分线的垂线,垂足为点Q,过点Q作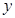 轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为
。
轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为
。