题目内容
19.已知函数f(x)是定义在R上的偶函数,且x1,x2∈[0,+∞)时,有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,若实数a满足f(log2a)+f(log${\;}_{\frac{1}{2}}$a)≤2f(1),则a的取值范围( )| A. | [1,2] | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,2] | D. | (0,2] |
分析 由题意可得,函数f(x)在[0,+∞)上单调递增,利用对数的运算性质化简所给的不等式可得 log2a≤1,由此求得a的范围.
解答 解:由题意可得,函数f(x)在[0,+∞)上单调递增,f(log2a)+f(log${\;}_{\frac{1}{2}}$a)≤2f(1),
即f(log2a)+f(${log}_{2}\frac{1}{a}$)≤2f(1),即 f(log2a)+f(-log2a)≤2f(1),
即2f(log2a)≤2f(1),即 f(log2a)≤f(1),∴-1≤log2a≤1,∴$\frac{1}{2}$≤a≤2,
故选:C.
点评 本题主要考查函数的单调性的判断和应用,对数的运算性质,属于基础题.

练习册系列答案
相关题目
14.如果MP,OM分别是角α=$\frac{3π}{16}$的正弦线和余弦线,那么下列结论正确的是( )
| A. | MP<OM<0 | B. | MP<0<OM | C. | MP>OM>0 | D. | OM>MP>0 |
3.已知f(x)是定义在R上的奇函数,当x<0时,f(x)=x2+2x,则函数$g(x)=f(x)+\frac{1}{2}x-1$零点的集合为( )
| A. | {1,-1,0} | B. | {-2,2,0} | C. | $\{2,-\frac{1}{2},\frac{{-5+\sqrt{41}}}{4}\}$ | D. | $\{2,\frac{1}{2},\frac{{-5-\sqrt{41}}}{4}\}$ |
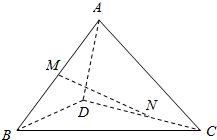 在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.
在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.