题目内容
10.等比数列{an}的各项均为正数,且2a1+3a2=1,${a_3}^2$=9a2a6.求数列{an}的通项公式.分析 根据等比数列的通项公式,建立方程组关系,求出首项和公比即可.
解答 解:由${a_3}^2$=9a2a6.得${a_3}^2$=9(a4)2.
∵等比数列{an}的各项均为正数,
∴a3=3a4,
即公比q=$\frac{{a}_{4}}{{a}_{3}}=\frac{1}{3}$,
由2a1+3a2=1得2a1+3×$\frac{1}{3}$a1=1,
即3a1=1,即a1=$\frac{1}{3}$,
则数列{an}的通项公式an=$\frac{1}{3}$•($\frac{1}{3}$)n-1=($\frac{1}{3}$)n.
点评 本题主要考查等比数列通项公式的求解,利用等比数列的性质建立方程组关系是解决本题的关键.

练习册系列答案
相关题目
2.已知函数f(x)的定义域是R,f′(x)是f(x)的导数.f(1)=-$\frac{5}{4}$,对?x∈R,有f′(x)≤-e(e=2.71828…是自然对数的底数).不等式f(x)<$\frac{1}{2}$x2lnx-$\frac{5}{4}$x2的解集是( )
| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | ($\frac{1}{2}$,1) |
5.已知 P:log2x>0,Q:x2-x>0,则P是Q的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | C. | 充要条件 | D. | 都不是 |
15.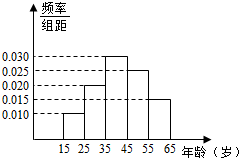 某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
 某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 | y |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.