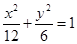题目内容
动点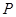 到两定点
到两定点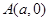 ,
,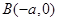 连线的斜率的乘积为
连线的斜率的乘积为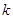 (
(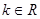 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
C
解析试题分析:由题设知直线PA与PB的斜率存在且均不为零
所以kPA•kPB=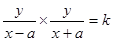 ,
,
整理得,点P的轨迹方程为kx2-y2=ka2(x≠±a);
① 当k>0,点P的轨迹是焦点在x轴上的双曲线(除去A,B两点)
② 当k=0,点P的轨迹是x轴(除去A,B两点)
③ 当-1<k<0时,点P的轨迹是焦点在x轴上的椭圆(除去A,B两点)
④当k=-1时,点P的轨迹是圆(除去A,B两点)
⑤当k<-1时,点P的轨迹是焦点在y轴上的椭圆(除去A,B两点).故选C.
考点:圆锥曲线的轨迹问题.
点评:本题考查圆锥曲线的轨迹问题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
双曲线 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
已知双曲线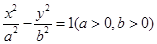 ,两渐近线的夹角为
,两渐近线的夹角为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.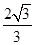 | B.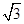 | C. | D.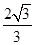 或 或 |
已知双曲线 的两条渐近线均与
的两条渐近线均与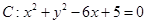 相切,则该双曲线离心率等于
相切,则该双曲线离心率等于
A.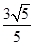 | B.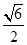 | C.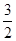 | D.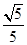 |
如图,F1,F2是双曲线C: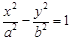 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与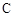 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
A.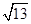 | B.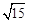 |
| C.2 | D.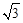 |
设抛物线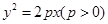 的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为
的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为
A.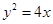 或 或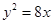 | B.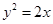 或 或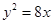 |
C.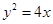 或 或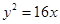 | D.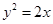 或 或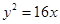 |
双曲线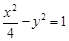 的顶点到渐进线的距离等于( )
的顶点到渐进线的距离等于( )
A.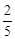 | B.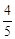 | C.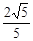 | D.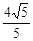 |
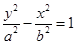 的一个焦点与抛物线
的一个焦点与抛物线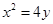 的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )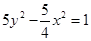
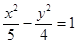
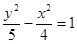
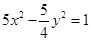
 的离心率为
的离心率为 ,双曲线
,双曲线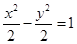 的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )
的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )