题目内容
已知双曲线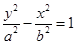 的一个焦点与抛物线
的一个焦点与抛物线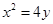 的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
A.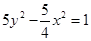 | B.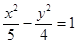 | C.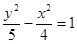 | D.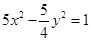 |
A
解析试题分析:抛物线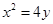 的焦点为
的焦点为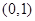 ,故双曲线的
,故双曲线的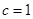 ,又
,又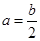 ,根据
,根据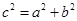 ,求得
,求得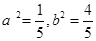 ,故双曲线的方程为
,故双曲线的方程为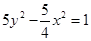 ,选A.
,选A.
考点:抛物线、双曲线的定义,双曲线的基本量之间的关系.

练习册系列答案
相关题目
设e是椭圆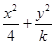 =1的离心率,且e∈(
=1的离心率,且e∈(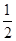 ,1),则实数k的取值范围是 ( )
,1),则实数k的取值范围是 ( )
| A.(0,3) | B.(3,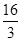 ) ) |
C.(0,3)∪(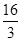 ,+∞) ,+∞) | D.(0,2) |
若双曲线 的离心率为2,则
的离心率为2,则 等于( )
等于( )
A. | B.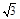 | C. | D. |
已知椭圆长轴长、短轴长和焦距成等差数列,则该椭圆的离心率是( )
A. | B. | C. | D. |
动点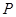 到两定点
到两定点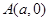 ,
,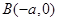 连线的斜率的乘积为
连线的斜率的乘积为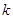 (
(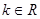 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
 的右焦点
的右焦点 作与
作与 轴垂直的直线,分别与双曲线及其渐近线交于点
轴垂直的直线,分别与双曲线及其渐近线交于点 (均在第一象限内),若
(均在第一象限内),若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )

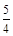





 ,
, 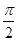 ), 以A, B为焦点且过点D的双曲线的离心率为e1, 以C, D为焦点且过点A的椭圆的离心率为e2, 设
), 以A, B为焦点且过点D的双曲线的离心率为e1, 以C, D为焦点且过点A的椭圆的离心率为e2, 设


 ,则双曲线的的离心率为( )
,则双曲线的的离心率为( )
