题目内容
当x=3时,不等式loga(x2-x-2)>loga(4x-6)(a>0且a≠1)成立,则此不等式的解集是
{x|2<x<4,x∈R}
{x|2<x<4,x∈R}
.分析:由已知中当x=3时,不等式loga(x2-x-2)>loga(4x-6)(a>0且a≠1)成立,根据函数单调性与底数的关系,可以判断出a的范围,进而结合对数式中真数必须大于0,及对数函数的单调性,可将原不等式化为一个关于x的整式不等式组,进而解得答案.
解答:解:∵当x=3时,x2-x-2=4<4x-6=6
而此时不等式loga(x2-x-2)>loga(4x-6)成立
故函数y=logax为减函数,则0<a<1
若loga(x2-x-2)>loga(4x-6)
则
即
解得2<x<4
故不等式loga(x2-x-2)>loga(4x-6)的解集为{x|2<x<4,x∈R}
故答案为{x|2<x<4,x∈R}
而此时不等式loga(x2-x-2)>loga(4x-6)成立
故函数y=logax为减函数,则0<a<1
若loga(x2-x-2)>loga(4x-6)
则
|
即
|
解得2<x<4
故不等式loga(x2-x-2)>loga(4x-6)的解集为{x|2<x<4,x∈R}
故答案为{x|2<x<4,x∈R}
点评:本题考查的知识点是对数函数图象与性质,其中根据对数式中真数必须大于0,及对数函数的单调性,将原不等式化为一个关于x的整式不等式组,是解答本题的关键,解答中易忽略真数大于0,而错解为{x|1<x<4,x∈R}

练习册系列答案
相关题目

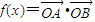 .
.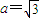 ,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;
,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;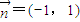 的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;
的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;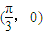 对称,且在
对称,且在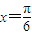 处f(x)取得最小值”.
处f(x)取得最小值”.