题目内容
设x,y为正数,则(x+y)(
+
)的最小值为( )
| 1 |
| x |
| 4 |
| y |
| A、6 | B、9 | C、12 | D、15 |
分析:函数中含有整式和分式的乘积,展开出现和的部分,而积为定值,利用基本不等式求最值
解答:解:x,y为正数,
(x+y)(
+
)≥1+4+
+
≥1+4+2
=9
当且仅当
=
时取得“=”
∴最小值为9
故选项为B.
(x+y)(
| 1 |
| x |
| 4 |
| y |
| y |
| x |
| 4x |
| y |
|
当且仅当
| y |
| x |
| 4x |
| y |
∴最小值为9
故选项为B.
点评:利用基本不等式求最值,需要满足的条件“一正,二定,三相等”

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
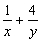 )的最小值为
)的最小值为